摘要：函数与方程在导数中的应用 例9．已知函数. (I) 求函数的单调区间; (Ⅱ)若不等式对任意的都成立(其中e是自然对数的底数). 求的最大值. 分析:由导数研究函数的单调性.求得函数的单调区间.不等式对任意的都成立可等价转化为不等式进而分离出来.不等式恒成立转为函数研究最值问题.可构造函数利用导数研究函数的单调性.从而求出最值. 解: (Ⅰ)函数的定义域是. 设则 令则 当时. 在上为增函数. 当x＞0时.在上为减函数. 所以h(x)在x=0处取得极大值.而h(0)=0,所以. 函数g(x)在上为减函数. 于是当时. 当x＞0时. 所以.当时.在上为增函数. 当x＞0时.在上为减函数. 故函数的单调递增区间为.单调递减区间为. (Ⅱ)不等式等价于不等式由知. 设则 由(Ⅰ)知.即 所以于是G(x)在上为减函数. 故函数G(x)在上的最小值为 所以a的最大值为 评注:第(1)问是为第二问铺垫的.在解答问题(2)时.不等式恒成立问题转化为函数研究最值.利用导数研究单调性.进而研究最值是解决函数最值问题的常用方法.理科的题目常常是超越方程或不等式.要利用导数解答问题.而文科的题基本上是含有参数的三次函数.如下一例题 例10．已知函数.且是奇函数．(Ⅰ)求.的值,(Ⅱ)求函数的单调区间． 分析:本题从函数的性质入手.利用奇函数的定义.确定函数的解析式..再由导数研究函数的单调性. 解:(Ⅰ)因为函数为奇函数. 所以.对任意的..即． 又 所以． 所以 解得． 得． 所以． 当时.由得． 变化时.的变化情况如下表: 0 0 单调递增 极大值 单调递减 极小值 单调递增 所以.当时.函数在上单调递增.在上单调递减.在上单调递增． 当时..所以函数在上单调递增． 评注:为奇函数是对任意的.都成立来说的.也就是恒等式.对应项的系数相等.从而确定系数.在研究含有参数的函数的单调性时往往要对参数在分界值处进行分类讨论.
网址：http://m.1010jiajiao.com/timu_id_3980603[举报]
已知函数
（1）若
的极值点，求实数a的值；
（2）若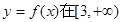
上为增函数，求实数a的取值范围；
（3）当
有实根，求实数b的最大值。
【解析】本试题主要是考查了导数在研究函数中的运用。主要是极值的概念和根据单调区间，求解参数的取值范围，以及利用函数与方程的思想求解参数b的最值。
查看习题详情和答案>>
已知函数
（I） 讨论f（x）的单调性；
（II） 设f（x）有两个极值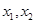点
若过两点
的直线I与x轴的交点在曲线
上，求α的值。
【解析】本试题考查了导数在研究函数中的运用。第一就是三次函数，通过求解导数，求解单调区间。另外就是运用极值的概念，求解参数值的运用。
【点评】试题分为两问，题面比较简单，给出的函数比较常规，，这一点对于同学们来说没有难度但是解决的关键还是要看导数的符号的实质不变，求解单调区间。第二问中，运用极值的问题，和直线方程的知识求解交点，得到参数的值。
（1）
查看习题详情和答案>>
已知函数f（x）=mx3+nx2（m、n∈R，m≠0）的图象在（2，f（2））处的切线与x轴平行．
（1）求n，m的关系式并求f（x）的单调减区间；
（2）证明：对任意实数0＜x1＜x2＜1，关于x的方程：f′(x)-
=0在（x1，x2）恒有实数解
（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f（x）是在闭区间[a，b]上连续不断的函数，且在区间（a，b）内导数都存在，则在（a，b）内至少存在一点x0，使得f′(x0)=
．如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：
当0＜a＜b时，
＜ln
＜
（可不用证明函数的连续性和可导性）．
查看习题详情和答案>>
（1）求n，m的关系式并求f（x）的单调减区间；
（2）证明：对任意实数0＜x1＜x2＜1，关于x的方程：f′(x)-
| f(x2)-f(x1) |
| x2-x1 |
（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f（x）是在闭区间[a，b]上连续不断的函数，且在区间（a，b）内导数都存在，则在（a，b）内至少存在一点x0，使得f′(x0)=
| f(b)-f(a) |
| b-a |
当0＜a＜b时，
| b-a |
| b |
| b |
| a |
| b-a |
| a |
在（x1,x2）恒有实数解
.如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明：
（可不用证明函数的连续性和可导性）
在（x1，x2）恒有实数解
．如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：
（可不用证明函数的连续性和可导性）．