17.(Ⅰ)期望为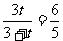 ,所以
,所以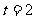 ,即盒中有 3个红球,2 个白球.3分
,即盒中有 3个红球,2 个白球.3分
(Ⅱ)由题可得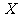 的取值为0,1,2,3.
┅┅4分
的取值为0,1,2,3.
┅┅4分
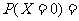
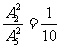 ,
,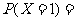
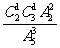 =
=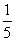 ,
,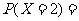
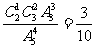 ,
,
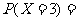
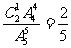 ┅┅10分
┅┅10分
所以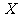 的分布列为
的分布列为
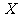 |
0 |
1 |
2 |
3 |
|
P |
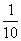 |
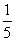 |
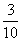 |
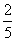 |
E(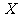 )
=
)
=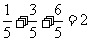 ┅┅12分
┅┅12分
答:白球的个数为2,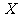 的数学期望为2 ┅┅┅┅┅┅13分
的数学期望为2 ┅┅┅┅┅┅13分
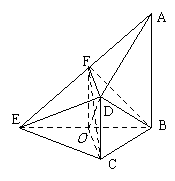
18解法1:(Ⅰ)证明:取BE的中点O,连OC,OF,DF,
则2OF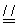 BA ………2分
BA ………2分
 ∵AB⊥平面BCE,CD⊥平面BCE,∴2CD
∵AB⊥平面BCE,CD⊥平面BCE,∴2CD 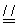 BA,
BA,
∴OF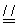 CD,∴OC∥FD………………4分
CD,∴OC∥FD………………4分
∵BC=CE,∴OC⊥BE,又AB⊥平面BCE.
∴OC⊥平面ABE. ∴FD⊥平面ABE.
从而平面ADE⊥平面ABE. …………6分
(Ⅱ)二面角A-EB-D与二面角F-EB-D相等,由(Ⅰ)知二面
角F-EB-D的平面角为∠FOD。BC=CE=2, ∠BCE=1200,OC⊥BE
得BO=OE=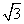 ,OC=1,∴OFDC为正方形,∴∠FOD=450,
,OC=1,∴OFDC为正方形,∴∠FOD=450,
∴二面角A-EB-D的余弦值为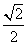 .…………10分
.…………10分
(Ⅲ)∵OFDC为正方形,∴CF⊥OD,CF⊥EB,∴CF⊥面EBD,
 ∴点F到平面BDE的距离为
∴点F到平面BDE的距离为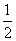 FC,∴点F到平面BDE的距离为
FC,∴点F到平面BDE的距离为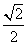 .……13分
.……13分
解法2:取BE的中点O,连OC.∵BC=CE, ∴OC⊥BE,
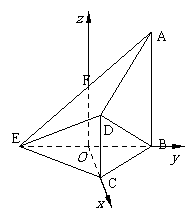
又AB⊥平面BCE. 以O为原点建立如图空间直角
坐标系O-xyz,
则由已知条件有: 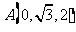 ,
,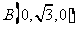 ,
,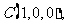
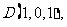
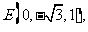
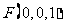 ………………2分
………………2分
设平面ADE的法向量为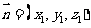 ,
,
则由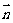 ·
·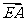

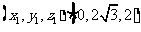
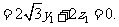
及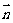 ·
·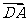

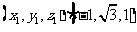
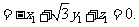
可取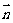

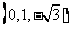 …………………… 4分
…………………… 4分
又AB⊥平面BCE,∴AB⊥OC,OC⊥平面ABE,
∴平面ABE的法向量可取为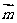 =
=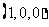 .
.
∵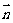 ·
·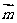

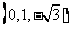 ·
·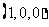 =0, ∴
=0, ∴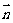 ⊥
⊥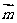 ,∴平面ADE⊥平面ABE.…… 6分
,∴平面ADE⊥平面ABE.…… 6分
(Ⅱ)设平面BDE的法向量为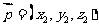 ,
,
则由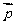 ·
·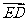

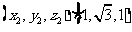
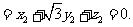
及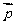 ·
·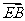

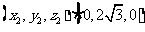
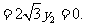 可取
可取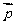

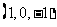 …… 7分
…… 7分
∵平面ABE的法向量可取为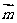 =
=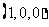 ………8分
………8分
∴锐二面角A-EB-D的余弦值为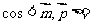
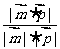 =
=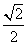 ,…… 9分
,…… 9分
∴二面角A-EB-D的余弦值为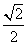 。 ………………10分
。 ………………10分
(Ⅲ)点F到平面BDE的距离为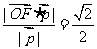 .………………13分
.………………13分
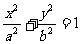 ,则
,则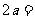
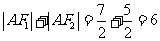 ,
,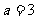 ………2分
………2分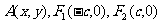 ,则
,则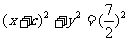 ,
,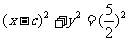 ,
,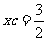 ,由抛物线定义可知
,由抛物线定义可知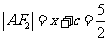 ,
,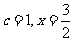 或
或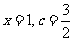 (舍去)
(舍去)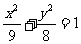 ,抛物线方程为
,抛物线方程为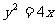 。 …………5分
。 …………5分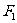 作垂直于
作垂直于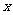 轴的直线
轴的直线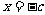 ,即抛物线的准线,
,即抛物线的准线,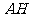 垂直于该准线,作
垂直于该准线,作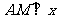 轴于
轴于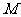 ,则由抛物线的定义得
,则由抛物线的定义得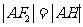 ,
,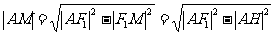
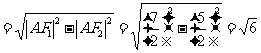
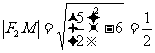 ,
,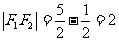 ,所以c=1,
,所以c=1,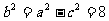
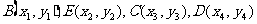 ,直线
,直线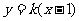 ,
,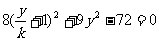 ,即
,即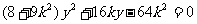 ,
,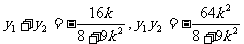 …………………………7分
…………………………7分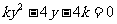 ,
,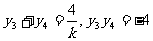 , …………………………8分
, …………………………8分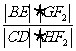 =
=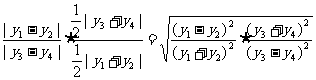
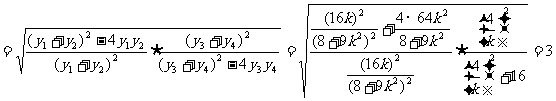 为定值。…………13分
为定值。…………13分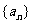 是等比数列,
是等比数列,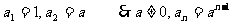
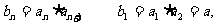 ……………………………………2分
……………………………………2分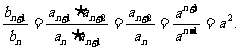
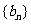 是以a为首项,
是以a为首项,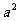 为公比的等比数列.…………………………6分
为公比的等比数列.…………………………6分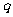 则
则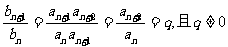
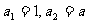
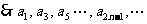 是以1为首项,q为公比的等比数列,
是以1为首项,q为公比的等比数列,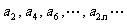 是以
是以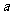 为首项,q为公比的等比数列.……………10分
为首项,q为公比的等比数列.……………10分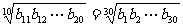
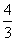 12.-9.8元
13.
12.-9.8元
13.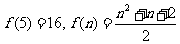
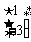 ,属于特征值3的一个特征向量为
,属于特征值3的一个特征向量为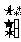 ,求矩阵A.
,求矩阵A.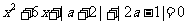 有实根,求
有实根,求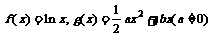
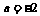 时,函数
时,函数 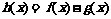 在其定义域内是增函数,
在其定义域内是增函数,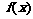 的图象C1 与函数
的图象C1 与函数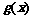 的图象C2 交于P,Q两点,过线段PQ的中点R作x轴的垂线分别交C1、C2于M、N两点,问是否存在点R,使C1 在M处的切线与C2 在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由。
的图象C2 交于P,Q两点,过线段PQ的中点R作x轴的垂线分别交C1、C2于M、N两点,问是否存在点R,使C1 在M处的切线与C2 在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由。 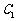 是以原点O为中心、
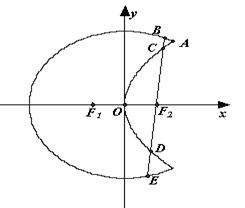
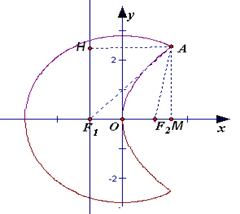
是以原点O为中心、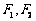 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线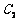 是以O为顶点、
是以O为顶点、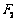 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线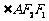 为钝角,若
为钝角,若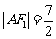 ,
,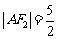 ,
,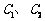 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问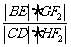 是否为定值?若是求出定值;若不是说明理由。
是否为定值?若是求出定值;若不是说明理由。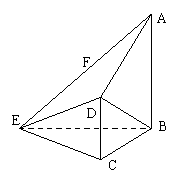 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,