摘要:17.(Ⅰ)期望为.所以.即盒中有 3个红球.2 个白球.3分 (Ⅱ)由题可得的取值为0.1.2.3. ┅┅4分 ,=,, ┅┅10分 所以的分布列为 0 1 2 3 P E() = ┅┅12分 答:白球的个数为2.的数学期望为2 ┅┅┅┅┅┅13分 18解法1:(Ⅰ)证明:取BE的中点O.连OC.OF.DF. 则2OFBA ---2分 ∵AB⊥平面BCE.CD⊥平面BCE.∴2CD BA. ∴OFCD.∴OC∥FD------4分 ∵BC=CE.∴OC⊥BE.又AB⊥平面BCE. ∴OC⊥平面ABE. ∴FD⊥平面ABE. 从而平面ADE⊥平面ABE. ----6分 (Ⅱ)二面角A-EB-D与二面角F-EB-D相等.由(Ⅰ)知二面 角F-EB-D的平面角为∠FOD.BC=CE=2, ∠BCE=1200.OC⊥BE 得BO=OE=.OC=1.∴OFDC为正方形.∴∠FOD=450. ∴二面角A-EB-D的余弦值为.----10分 (Ⅲ)∵OFDC为正方形.∴CF⊥OD.CF⊥EB.∴CF⊥面EBD. ∴点F到平面BDE的距离为FC.∴点F到平面BDE的距离为.--13分 解法2:取BE的中点O.连OC.∵BC=CE, ∴OC⊥BE. 又AB⊥平面BCE. 以O为原点建立如图空间直角 坐标系O-xyz. 则由已知条件有: .. ------2分 设平面ADE的法向量为. 则由· 及· 可取 -------- 4分 又AB⊥平面BCE.∴AB⊥OC.OC⊥平面ABE. ∴平面ABE的法向量可取为=. ∵··=0, ∴⊥.∴平面ADE⊥平面ABE.-- 6分 (Ⅱ)设平面BDE的法向量为. 则由· 及·可取-- 7分 ∵平面ABE的法向量可取为= ---8分 ∴锐二面角A-EB-D的余弦值为=.-- 9分 ∴二面角A-EB-D的余弦值为. ------10分 (Ⅲ)点F到平面BDE的距离为.------13分
网址:http://m.1010jiajiao.com/timu3_id_532719[举报]
已知甲盒中仅有1个球且为红球,乙盒中有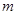 个红球和
个红球和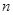 个篮球
个篮球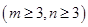 ,从乙盒中随机抽取
,从乙盒中随机抽取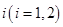 个球放入甲盒中.
个球放入甲盒中.
(a)放入 个球后,甲盒中含有红球的个数记为
个球后,甲盒中含有红球的个数记为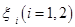 ;
;
(b)放入 个球后,从甲盒中取1个球是红球的概率记为
个球后,从甲盒中取1个球是红球的概率记为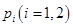 .
.
则
A.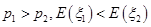 | B.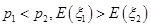 |
C.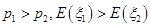 | D.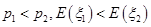 |
有红色和黑色两个盒子,红色盒中有6张卡片,其中一张标有数字0,两张标有数字1,三张标有数字2;黑色盒中有7张卡片,其中4张标有数字0,一张标有数字1,两张标有数字2.现从红色盒中任意取1张卡片(每张卡片被抽出的可能性相等),黑色盒中任意取2张卡片(每张卡片抽出的可能性相等),共取3张卡片.
(Ⅰ)求取出的3张卡片都标有数字0的概率;
(Ⅱ)求取出的3张卡片数字之积是4的概率;
(Ⅲ)记ξ为取出的3张卡片的数字之积,求ξ的概率分布及数学期望Eξ. 查看习题详情和答案>>
(Ⅰ)求取出的3张卡片都标有数字0的概率;
(Ⅱ)求取出的3张卡片数字之积是4的概率;
(Ⅲ)记ξ为取出的3张卡片的数字之积,求ξ的概率分布及数学期望Eξ. 查看习题详情和答案>>
某单位举办2010年上海世博会知识宣传活动,进行现场抽奖.盒中装有10张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(1)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人答:我只知道,从盒中抽取两张都是“世博会会徽“卡的概率是
,求抽奖者获奖的概率;
(2)现有甲、乙、丙、丁四人依次抽奖,用ξ表示获奖的人数,求ξ的分布列及期望. 查看习题详情和答案>>
(1)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人答:我只知道,从盒中抽取两张都是“世博会会徽“卡的概率是
| 2 | 15 |
(2)现有甲、乙、丙、丁四人依次抽奖,用ξ表示获奖的人数,求ξ的分布列及期望. 查看习题详情和答案>>