0 52698 52706 52712 52716 52722 52724 52728 52734 52736 52742 52748 52752 52754 52758 52764 52766 52772 52776 52778 52782 52784 52788 52790 52792 52793 52794 52796 52797 52798 52800 52802 52806 52808 52812 52814 52818 52824 52826 52832 52836 52838 52842 52848 52854 52856 52862 52866 52868 52874 52878 52884 52892 447348
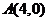 的直线
的直线 与曲线
与曲线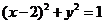 有公共点,则直线
有公共点,则直线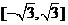 B.
B.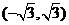 C.
C.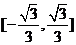 D.
D.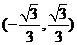
 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为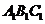 ,
,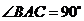 ,
,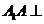 平面
平面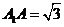 ,
,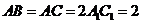 ,
,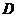 为
为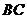 中点.
中点.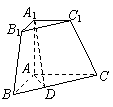 (Ⅰ)证明:平面
(Ⅰ)证明:平面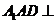 平面
平面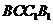 ;
;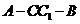 的大小.
的大小.
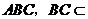 平面
平面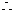
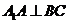 .在
.在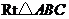 中,
中,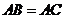 ,
,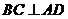 .又
.又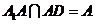 ,
,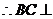 平面
平面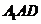 ,
,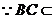 平面
平面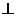 平面
平面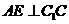 交
交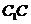 于
于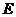 点,连接
点,连接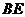 ,
, 由已知得
由已知得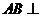 平面
平面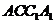 .
.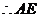 是
是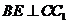 ,
,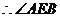 为二面角
为二面角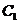 作
作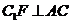 交
交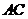 于
于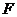 点,
点,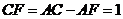 ,
,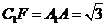 ,
,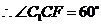 .
.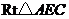 中,
中,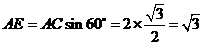 .
.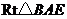 中,
中,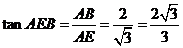 .
.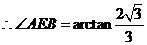 ,
,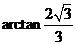 .
.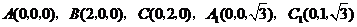 ,
,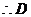 点坐标为
点坐标为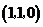 .
.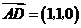 ,
, .
.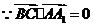 ,
,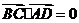 ,
,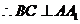 ,
,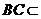 平面
平面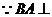 平面
平面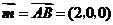 为平面
为平面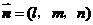 ,则
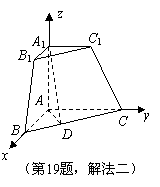
,则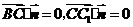 .
.
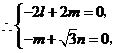
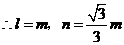 ,
,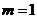 ,则
,则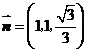 ,
,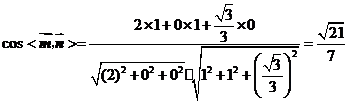 ,
,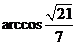 为所求.
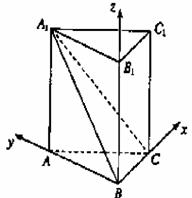
为所求.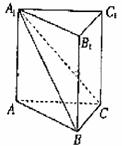 如图,在直三棱柱
如图,在直三棱柱 中,平面
中,平面 侧面
侧面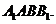
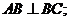
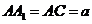 ,直线AC与平面
,直线AC与平面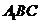 所成的角为
所成的角为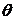 ,二面角
,二面角
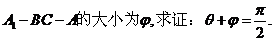
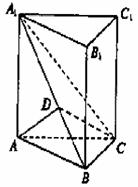 得AD⊥平面
得AD⊥平面 平面A1BC
平面A1BC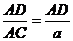 ,在RtΔADA1中,sin∠AA1D=
,在RtΔADA1中,sin∠AA1D=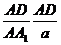 ,
,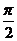 ,故θ+j=
,故θ+j=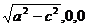 ),
), A1(0,c,a),于是
A1(0,c,a),于是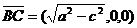 ,
,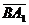 =(0,c,a),
=(0,c,a),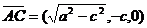 ,
,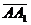 =(0,c,a)
=(0,c,a)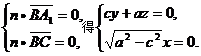
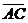 =ac>0,
=ac>0,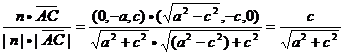 ,
,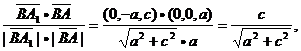
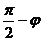 ),又0<q,j<
),又0<q,j<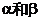 为平面,
为平面,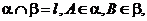 AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角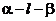 的大小为
的大小为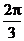 ,求:
,求: 的距离;
的距离;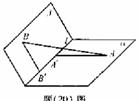
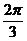 .因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=
.因此在Rt△BB′D中,BB′=2,∠BB′D=π-∠BB′C=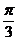 ,BD=BB′·sinBB′D
,BD=BB′·sinBB′D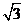 .
.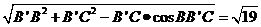 .
.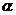 ,且DC
,且DC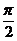 ,sinBAC=
,sinBAC=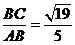 .
.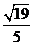 .
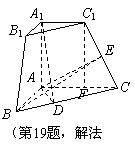
. BCF=
BCF=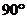 ,AD=
,AD=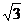 ,EF=2。
,EF=2。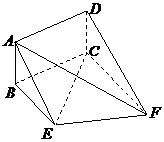 (Ⅰ)求证:AE//平面DCF;
(Ⅰ)求证:AE//平面DCF;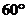 ?
? 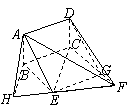 (Ⅰ)证明:过点
(Ⅰ)证明:过点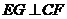 交
交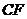 于
于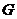 ,连结
,连结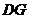 ,
,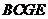 为矩形,
为矩形,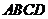 为矩形,
为矩形,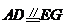 ,从而四边形
,从而四边形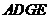 为平行四边形,
为平行四边形,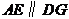 .
.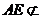 平面
平面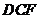 ,
,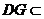 平面
平面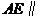 平面
平面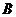 作
作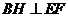 交
交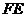 的延长线于
的延长线于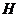 ,连结
,连结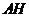 .
.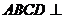 平面
平面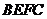 ,
,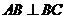 ,得
,得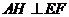 .
.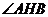 为二面角
为二面角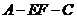 的平面角.
的平面角.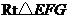 中,因为
中,因为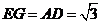 ,
,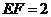 ,所以
,所以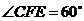 ,
,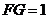 .
.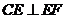 ,所以
,所以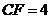 ,
,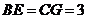 .
.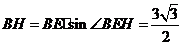 .
.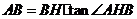 ,
,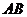 为
为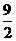 时,二面角
时,二面角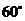 .
. 方法二:如图,以点
方法二:如图,以点 为坐标原点,以
为坐标原点,以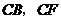 和
和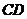 分别作为
分别作为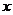 轴,
轴,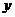 轴和
轴和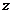 轴,建立空间直角坐标系
轴,建立空间直角坐标系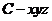 .
.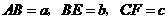 ,
,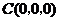 ,
,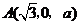 ,
,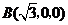 ,
,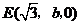 ,
,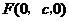 .
.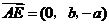 ,
,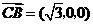 ,
,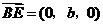 ,
,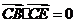 ,
,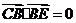 ,从而
,从而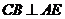 ,
,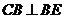 ,
,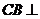 平面
平面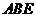 .
.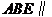 平面
平面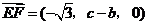 ,
,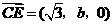 ,
,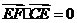 ,
,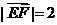 ,从而
,从而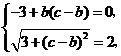
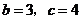 .
.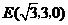 ,
,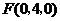 .
.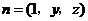 与平面
与平面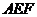 垂直,
垂直,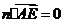 ,
,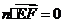 ,
,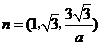 .
.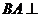 平面
平面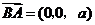 ,
,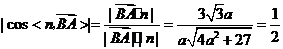 ,
,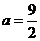 .
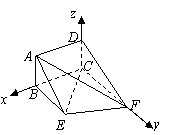
.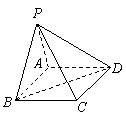 如图,在四棱锥
如图,在四棱锥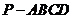 中,底面
中,底面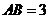 ,
,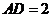 ,
,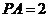 ,
,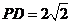 ,
,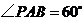 .
.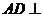 平面
平面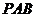 ;
;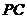 与
与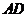 所成的角的大小;
所成的角的大小;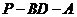 的大小.
的大小.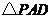 中,由题设
中,由题设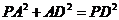 ,于是
,于是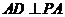 .在矩形
.在矩形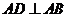 ,又
,又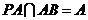 ,所以
,所以 ,所以
,所以 (或其补角)是异面直线
(或其补角)是异面直线 中,由余弦定理得
中,由余弦定理得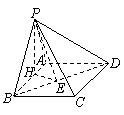
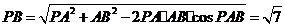 .
.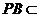 平面
平面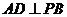 ,因而
,因而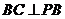 ,于是
,于是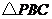 是直角三角形,
是直角三角形,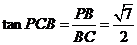 .
. .
.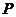 作
作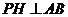 于
于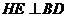 于
于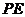 .
.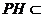 平面
平面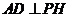 .又
.又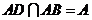 ,因而
,因而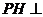 平面
平面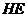 为
为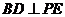 .从而
.从而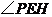 是二面角
是二面角 ,
,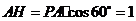 ,
,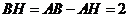 ,
,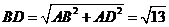 ,
,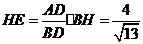 .
. 中,
中,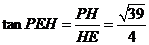 .
.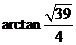 .
. 平面
平面 与
与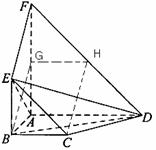
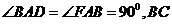
 ,
, ,
,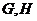 分别为
分别为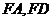 的中点
的中点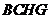 是平行四边形;
是平行四边形;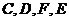 四点是否共面?为什么?
四点是否共面?为什么?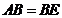 ,证明:平面
,证明:平面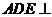 平面
平面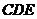 ;
;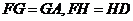
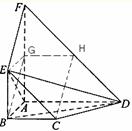 所以
所以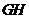
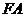 的中点知,
的中点知,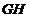 ,所以
,所以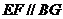
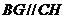 ,所以
,所以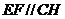 ,故
,故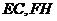 共面。又点
共面。又点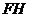 上
上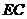 ,由
,由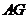 及
及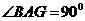 知
知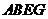 是正方形
是正方形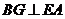 。由题设知
。由题设知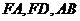 两两垂直,故
两两垂直,故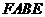 ,
,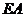 是
是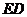 在平面
在平面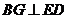
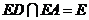 ,所以
,所以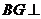 平面
平面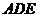
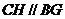 ,所以
,所以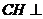 平面
平面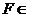 平面
平面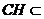 平面
平面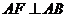 ,得
,得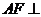 平面
平面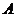 为坐标原点,射线
为坐标原点,射线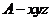
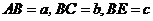 ,则由题设得
,则由题设得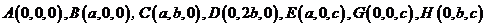
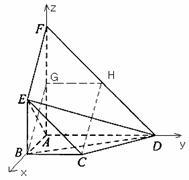 所以
所以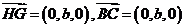
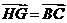
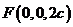 ,所以
,所以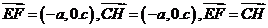 又
又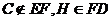 ,故
,故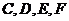 四点共面。
四点共面。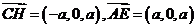
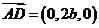 ,因此
,因此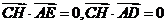
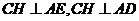
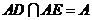 ,所以
,所以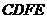 ,得平面
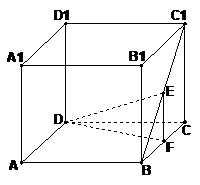
,得平面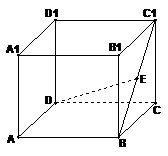 如图,在棱长为2的正方体
如图,在棱长为2的正方体 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
 ∵
∵
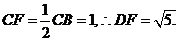 …………………………..8分
…………………………..8分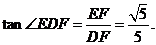 ……………..10分
……………..10分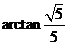 ….12分
….12分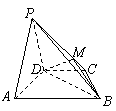 如图,在四棱锥
如图,在四棱锥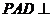 平面
平面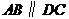 ,
,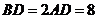 ,
,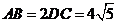 .
.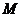 是
是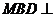 平面
平面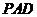 ;
;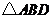 中,
中,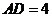 ,
,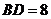 ,
,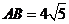 ,
,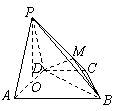 所以
所以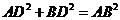 .
.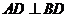 .
. 平面
平面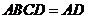 ,
,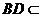 平面
平面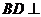 平面
平面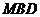 ,
,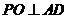 交
交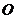 ,
,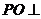 平面
平面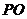 为四棱锥
为四棱锥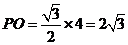 .
.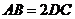 ,
,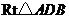 中,斜边
中,斜边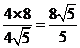 ,
,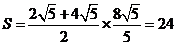 .
.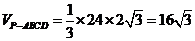 .
.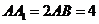 ,点
,点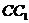 上且
上且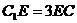 .
.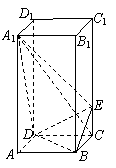 (Ⅰ)证明:
(Ⅰ)证明: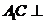 平面
平面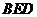 ;
;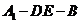 的大小.
的大小.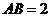 ,
,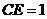 .
.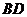 于点
于点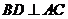 .
.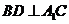 .····················································································· 3分
.····················································································· 3分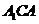 内,连结
内,连结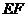 交
交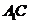 于点
于点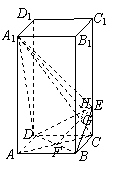 由于
由于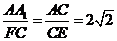 ,
,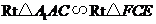 ,
,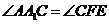 ,
,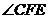 与
与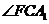 互余.
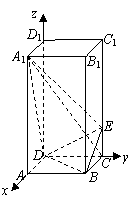
互余.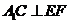 .
.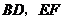 都垂直,
都垂直,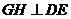 ,垂足为
,垂足为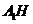 .由三垂线定理知
.由三垂线定理知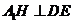 ,
,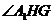 是二面角
是二面角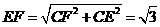 ,
,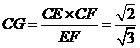 ,
,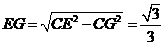 .
.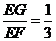 ,
,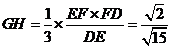 .
.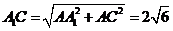 ,
,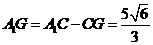 .
.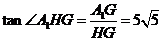 .
. 所以二面角
所以二面角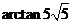 .··························································· 12分
.··························································· 12分  为
为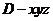 .
.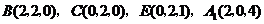 .
.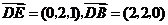 ,
,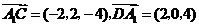 .··································· 3分
.··································· 3分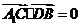 ,
,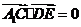 ,
,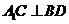 ,
,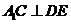 .
.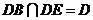 ,
,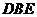 .································································································ 6分
.································································································ 6分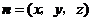 是平面
是平面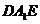 的法向量,则
的法向量,则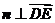 ,
,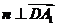 .
.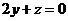 ,
,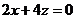 .
.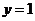 ,则
,则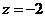 ,
,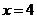 ,
,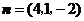 .······························································· 9分
.······························································· 9分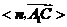 等于二面角
等于二面角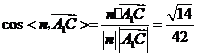 .
.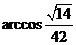 .·························································· 12分
.·························································· 12分