摘要:19.. 如图.在直三棱柱中.平面侧面 (Ⅰ)求证: (Ⅱ)若.直线AC与平面所成的角为.二面角 (Ⅰ)证明:如右图.过点A在平面A1ABB1内作AD⊥A1B于D.则 由平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B. 得AD⊥平面 A1BC.又BC平面A1BC 所以AD⊥BC. 因为三棱柱ABC-A1B1C1是直三棱柱, 则AA1⊥底面ABC,所以AA1⊥BC. 又AA1∩AD=A,从而BC⊥侧面A1ABB1, 又AB侧面A1ABB1. 故AB⊥BC. (Ⅱ)证法1:连接CD,则由(Ⅰ)知∠ACD就是直线AC与平面A1BC所成的角.∠ABA1就是二面角A1-BC-A的颊角.即∠ACD=θ.∠ABA1=j. 于是在RtΔADC中.sinθ=,在RtΔADA1中.sin∠AA1D=, ∴sinθ=sin∠AA1D,由于θ与∠AA1D都是锐角.所以θ=∠AA1D. 又由RtΔA1AB知.∠AA1D+j=∠AA1B+j=.故θ+j=. 证法2:由(Ⅰ)知.以点B为坐标原点.以BC.BA.BB1所在的直线分别为x轴.y轴.z轴.建立如图所示的空间直角坐标系. 设AB=c(c<a=.则B.A(0,c,0).C(), A1(0,c,a).于是.=(0.c,a), ,=(0,c,a) 设平面A1BC的一个法向量为n=(x,y,z), 则由 可取n=(0.-a.c).于是 n·=ac>0.与n的夹角b为锐角,则b与q互为余角. sinq=cosb=, cosj= 所以sinq=cosj=sin(),又0<q.j<.所以q+j=.
网址:http://m.1010jiajiao.com/timu3_id_527958[举报]
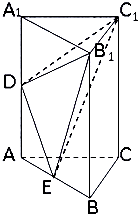 如图,在直三棱柱ABC-A1B1C1中,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积与三棱柱ABC-A1B1C1的体积之比是( )
如图,在直三棱柱ABC-A1B1C1中,E是AB的中点,D是AA1的中点,则三棱锥D-B1C1E的体积与三棱柱ABC-A1B1C1的体积之比是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 (2013•乐山二模)如图,在直三棱柱ABC-A1B1C1中,A1A=AB=2,BC=1,∠ABC=90°,若规定主(正)视方向垂直平面ACC1A1,则此三棱柱的左视图的面积为( )
(2013•乐山二模)如图,在直三棱柱ABC-A1B1C1中,A1A=AB=2,BC=1,∠ABC=90°,若规定主(正)视方向垂直平面ACC1A1,则此三棱柱的左视图的面积为( ) 如图,在直三棱柱A1B1C1-ABC中,
如图,在直三棱柱A1B1C1-ABC中, 如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )
如图,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,则BC1与平面AB B1 A1所成角的正弦值是( )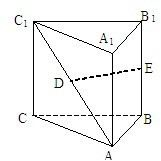 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=