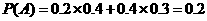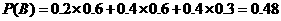24.(陕西理)(18).(本小题满分12分)
某射击测试规则为:每人最多射击3次,击中目标即终止射击,第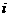 次击中目标得
次击中目标得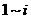
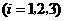 分,3次均未击中目标得0分.已知某射手每次击中目标的概率为0.8,其各次射击结果互不影响.
分,3次均未击中目标得0分.已知某射手每次击中目标的概率为0.8,其各次射击结果互不影响.
(1)求该射手恰好射击两次的概率;
(2)该射手的得分记为 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
解:(1)设该射手第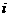 次击中目标的事件为
次击中目标的事件为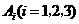 ,则
,则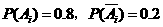 ,
,
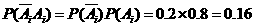 .
.
(2) 可能取的值为0,1,2,3.
可能取的值为0,1,2,3.  的分布列为
的分布列为
 |
0 |
1 |
2 |
3 |
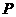 |
0.008 |
0.032 |
0.16 |
0.8 |
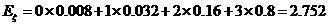
22.(山东理)(18)(本小题满分12分)甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分。假设甲队中每人答对的概率均为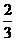 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为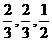 且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
且各人正确与否相互之间没有影响.用ε表示甲队的总得分.
(1)求随机变量ε分布列和数学期望;
(2) 用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
(1)解法一:由题意知,ε的可能取值为0,1,2,3,且
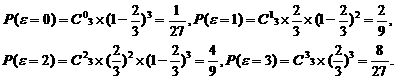
所以ε的分布列为
|
ε |
0 |
1 |
2 |
3 |
|
P |
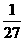 |
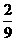 |
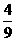 |
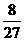 |
ε的数学期望为 Eε=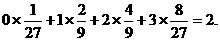
解法二:根据题设可知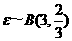
因此ε的分布列为
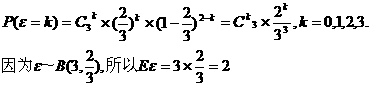
(2)解法一:用C表示“甲得2分乙得1分”这一事件,用D表示“甲得3分乙得0分”这一事件,所以AB=C∪D,且C、D互斥,又
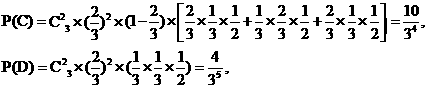
由互斥事件的概率公式得
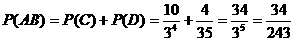
 解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“已队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故事
解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“已队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故事
P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).
=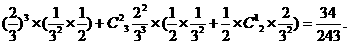
19.(全国Ⅰ理;文只做(1))20.(本小题满分12分)已知5只动物中有1只患有某种疾病,需要通过化验血液来确定患病的动物.血液化验结果呈阳性的即为患病动物,呈阴性即没患病.下面是两种化验方法:
方案甲:逐个化验,直到能确定患病动物为止.
方案乙:先任取3只,将它们的血液混在一起化验.若结果呈阳性则表明患病动物为这3只中的1只,然后再逐个化验,直到能确定患病动物为止;若结果呈阴性则在另外2只中任取1只化验.
(1)求依方案甲所需化验次数不少于依方案乙所需化验次数的概率;
(2) 表示依方案乙所需化验次数,求
表示依方案乙所需化验次数,求 的期望.
的期望.
解:(1)对于甲:
|
次数 |
1 |
2 |
3 |
4 |
5 |
|
概率 |
0.2 |
0.2 |
0.2 |
0.2 |
0.2 |
对于乙:
|
次数 |
2 |
3 |
4 |
|
概率 |
0.4 |
0.4 |
0.2 |
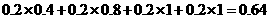 .
.
(2) 表示依方案乙所需化验次数,
表示依方案乙所需化验次数, 的期望为
的期望为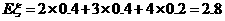
16.(辽宁文)(18).(本小题满分12分)
某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
|
周销售量 |
2 |
3 |
4 |
|
频数 |
20 |
50 |
30 |
(1)根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
(2)若以上述频率作为概率,且各周的销售量相互独立,求
(ⅰ)4周中该种商品至少有一周的销售量为4吨的概率;
(ⅱ)该种商品4周的销售量总和至少为15吨的概率.
解:(1)周销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3.
(2)由题意知一周的销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3,故所求的概率为
(ⅰ)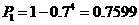 .
.
(ⅱ)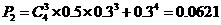 .
.
15.(辽宁理)(18).某批发市场对某种商品的周销售量(单位:吨)进行统计,最近100周的统计结果如下表所示:
|
周销售量 |
2 |
3 |
4 |
|
频数 |
20 |
50 |
30 |
⑴根据上面统计结果,求周销售量分别为2吨,3吨和4吨的频率;
⑵已知每吨该商品的销售利润为2千元, 表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求
表示该种商品两周销售利润的和(单位:千元),若以上述频率作为概率,且各周的销售量相互独立,求 的分布列和数学期望.
的分布列和数学期望.
解:(1)周销售量为2吨,3吨和4吨的频率分别为0.2,0.5和0.3.
(2) 的可能值为8,10,12,14,16,且
的可能值为8,10,12,14,16,且
P( =8)=0.22=0.04,
=8)=0.22=0.04,
P( =10)=2×0.2×0.5=0.2,
=10)=2×0.2×0.5=0.2,
P( =12)=0.52+2×0.2×0.3=0.37,
=12)=0.52+2×0.2×0.3=0.37,
P( =14)=2×0.5×0.3=0.3,
=14)=2×0.5×0.3=0.3,
P( =16)=0.32=0.09.
=16)=0.32=0.09.
 的分布列为
的分布列为
 |
8 |
10 |
12 |
14 |
16 |
|
P |
0.04 |
0.2 |
0.37 |
0.3 |
0.09 |
F =8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元)
=8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4(千元)
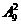 种结果,第一次摸出黑球、第二次摸出白球有
种结果,第一次摸出黑球、第二次摸出白球有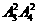 种结果,则所求概率
种结果,则所求概率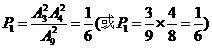 .
.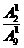 ,第二次摸出红球的概率为
,第二次摸出红球的概率为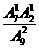 ,第三次摸出红球的概率为
,第三次摸出红球的概率为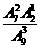 ,则摸球次数不超过3次的概率为
,则摸球次数不超过3次的概率为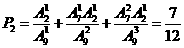 .
. 通晓日语,
通晓日语,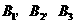 通晓俄语,
通晓俄语,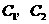 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组. 被选中的概率;
被选中的概率;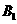 和
和 不全被选中的概率.
不全被选中的概率.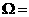 {
{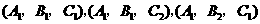 ,
,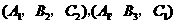 ,
,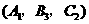 ,
,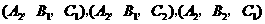 ,
,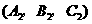 ,
,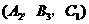 ,
,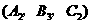 ,
,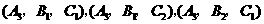 ,
,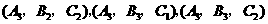 }
} 表示“
表示“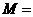 {
{ }
}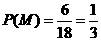 .
. 表示“
表示“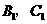 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件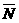 表示“
表示“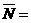 {
{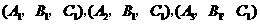 },事件
},事件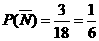 ,由对立事件的概率公式得
,由对立事件的概率公式得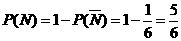 .
.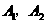 分别表示甲击中9环,10环,
分别表示甲击中9环,10环,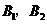 分别表示乙击中8环,9环,
分别表示乙击中8环,9环, 表示在一轮比赛中甲击中的环数多于乙击中的环数,
表示在一轮比赛中甲击中的环数多于乙击中的环数,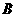 表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数,
表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数,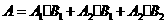 ,
,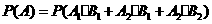
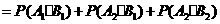
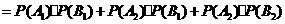
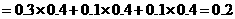 .
.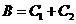 ,
,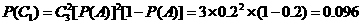 ,
,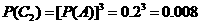 ,
,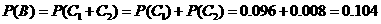 .
.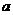 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10
000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10
000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为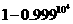 .
.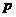 ;
;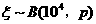 .
.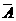 发生当且仅当
发生当且仅当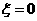 ,
, 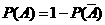
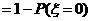
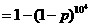 ,
,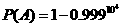 ,故
,故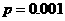 .
. 元,支出是赔偿金总额与成本的和.
元,支出是赔偿金总额与成本的和.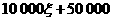 ,
,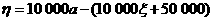 ,
,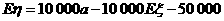 ,
,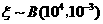 知,
知,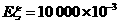 ,
,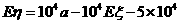
 .
.
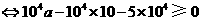
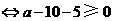
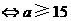 (元).
(元).