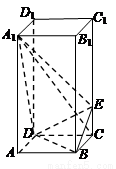摘要:12. 如图.正四棱柱中..点在上且. (Ⅰ)证明:平面, (Ⅱ)求二面角的大小. 解法一: 依题设... (Ⅰ)连结交于点.则. 由三垂线定理知..····················································································· 3分 在平面内.连结交于点. 由于. 故.. 与互余. 于是. 与平面内两条相交直线都垂直. 所以平面.································································································ 6分 (Ⅱ)作.垂足为.连结.由三垂线定理知. 故是二面角的平面角.································································· 8分 . .. .. 又.. . 所以二面角的大小为.··························································· 12分 解法二: 以为坐标原点.射线为轴的正半轴. 建立如图所示直角坐标系. 依题设.. ..··································· 3分 (Ⅰ)因为.. 故.. 又. 所以平面.································································································ 6分 (Ⅱ)设向量是平面的法向量.则 .. 故.. 令.则...······························································· 9分 等于二面角的平面角. . 所以二面角的大小为.·························································· 12分
网址:http://m.1010jiajiao.com/timu3_id_527951[举报]
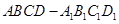 中,
中,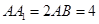 ,点
,点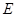 在
在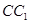 上且
上且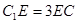 .
.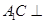 平面
平面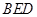 ;
;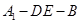 的余弦值大小.
的余弦值大小.


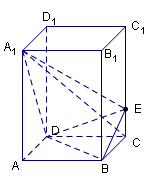
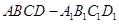 中,
中,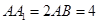 ,点
,点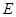 在
在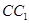 上且
上且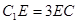
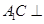 平面
平面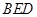 ;
;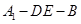 的余弦值.
的余弦值.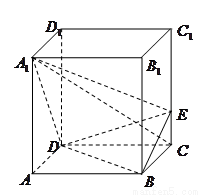
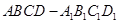 中,
中,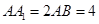 ,点
,点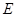 在
在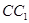 上且
上且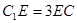
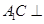 平面
平面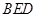 ;(2)求二面角
;(2)求二面角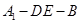 的余弦值
的余弦值