摘要:16. 如图.在四棱锥中.底面是矩形.已知..... (Ⅰ)证明平面, (Ⅱ)求异面直线与所成的角的大小, (Ⅲ)求二面角的大小. (Ⅰ)证明:在中.由题设...可得.于是.在矩形中..又.所以平面. (Ⅱ)解:由题设..所以是异面直线与所成的角. 在中.由余弦定理得 . 由(Ⅰ)知平面.平面. 所以.因而.于是是直角三角形. 故. 所以异面直线与所成的角的大小为. (Ⅲ)解:过点作于.过点作于.连结. 因为平面.平面.所以.又.因而平面.故为在平面内的射影.由三垂线定理可知..从而是二面角的平面角. 由题设可得. .. .. . 于是在中.. 所以二面角的大小为.
网址:http://m.1010jiajiao.com/timu3_id_527955[举报]
(2009江西卷文)(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() .以
.以![]() 的中点
的中点![]() 为球心、
为球心、![]() 为直径的球面交
为直径的球面交![]() 于点
于点![]() .
.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角;
所成的角;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.

查看习题详情和答案>>
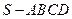 中,底面
中,底面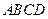 是正方形,
是正方形,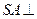 底面
底面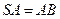 , 点
, 点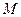 是
是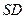 的中点,
的中点,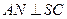 ,且交
,且交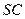 于点
于点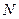 .
.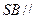 平面
平面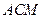 ;
;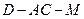 的余弦值大小;
的余弦值大小;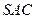 ⊥平面
⊥平面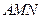 .
.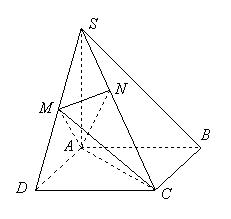
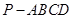 中,
中,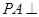 底面
底面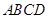 ,
,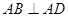 ,
,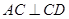 ,
,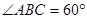 ,
,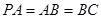 .
.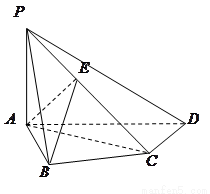
 平面
平面 ;
;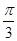 ,并说明理由.
,并说明理由.
 中,底面
中,底面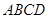 是正方形,侧棱
是正方形,侧棱 =2,
=2, ,垂足为F。
,垂足为F。