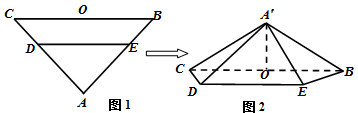
摘要:15. 如图.平面平面.四边形与都是直角梯形. ..分别为的中点 (Ⅰ)证明:四边形是平行四边形, (Ⅱ)四点是否共面?为什么? (Ⅲ)设.证明:平面平面, [解1]:(Ⅰ)由题意知. 所以 又.故 所以四边形是平行四边形. (Ⅱ)四点共面.理由如下: 由.是的中点知..所以 由(Ⅰ)知.所以.故共面.又点在直线上 所以四点共面. (Ⅲ)连结.由.及知是正方形 故.由题设知两两垂直.故平面. 因此是在平面内的射影.根据三垂线定理. 又.所以平面 由(Ⅰ)知.所以平面. 由(Ⅱ)知平面.故平面.得平面平面 [解2]:由平面平面..得平面. 以为坐标原点.射线为轴正半轴.建立如图所示的直角坐标系 (Ⅰ)设.则由题设得 所以 于是 又点不在直线上 所以四边形是平行四边形. (Ⅱ)四点共面.理由如下: 由题设知.所以 又.故四点共面. (Ⅲ)由得.所以 又.因此 即 又.所以平面 故由平面.得平面平面
网址:http://m.1010jiajiao.com/timu3_id_527954[举报]
 如图所示,在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°,则异面直线BC与PA所成角的余弦值是( )
如图所示,在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°,则异面直线BC与PA所成角的余弦值是( )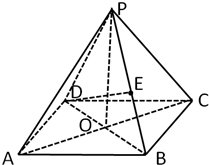 如图所示,在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°,E是PB的中点,则异面直线DE与PA所成角的余弦值是( )
如图所示,在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°,E是PB的中点,则异面直线DE与PA所成角的余弦值是( )| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
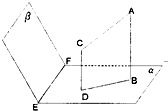 9、如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别是B、D,如果增加一个条件,就能推出BD⊥EF,这个条件不可能是下面四个选顶中的( )
9、如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别是B、D,如果增加一个条件,就能推出BD⊥EF,这个条件不可能是下面四个选顶中的( )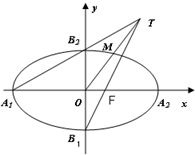 如图,在平面直角坐标系xoy中,A1,A2,B1,B2为椭圆
如图,在平面直角坐标系xoy中,A1,A2,B1,B2为椭圆