两角和与差的三角函数
[例1]
已知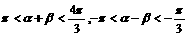 ,求
,求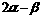 的范围。
的范围。
解:设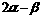 =
=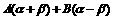 ,(A、B为待定的系数),则
,(A、B为待定的系数),则
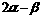 =
=
比较系数 ∴
∴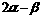 =
=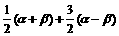
从而可得: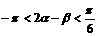
[例2]
设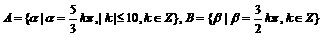 ,求
,求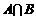 的解的终边相同的角的集合。
的解的终边相同的角的集合。
解:先写出A与B的交,再写出终边相同的角的集合。
设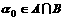 ,则
,则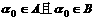 ;所以
;所以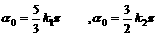
∴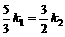 ,即
,即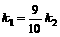 ,由于
,由于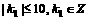
∴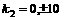 ;因此
;因此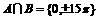
因此所有与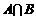 的角的终边相同的角的集合为
的角的终边相同的角的集合为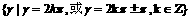
[例3]
已知 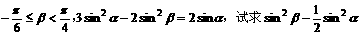 的最值。
的最值。
解:∵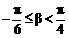 ∴-
∴-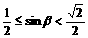 ,
,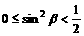 ∴
∴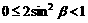
∵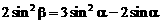 ∴
∴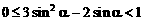
即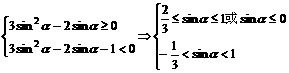
∴ 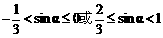
y=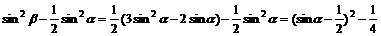
当sina∈[ ,1]时函数y递增,∴当sina=
,1]时函数y递增,∴当sina=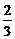 时 ymin=
时 ymin=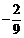 ;
;
当sina∈(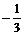 ,0)时,函数y递减,∴当sina=0时,ymin=
,0)时,函数y递减,∴当sina=0时,ymin=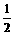
∴ 故当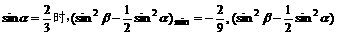 无最大值。
无最大值。
[例4]
求值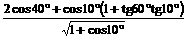
解:
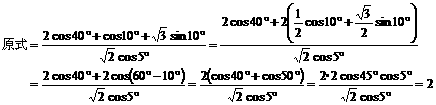
[例5]
已知 <β<α<
<β<α<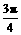 ,cos(α-β)=
,cos(α-β)=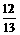 ,sin(α+β)=-
,sin(α+β)=- ,求sin2α的值_________.
,求sin2α的值_________.
解法一:∵ <β<α<
<β<α<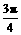 ,∴0<α-β<
,∴0<α-β<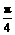 .π<α+β<
.π<α+β<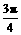 ,
,
∴sin(α-β)=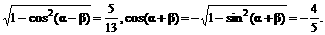
∴sin2α=sin[(α-β)+(α+β)]
=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)
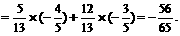
解法二:∵sin(α-β)=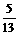 ,cos(α+β)=-
,cos(α+β)=-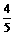 ,
,
∴sin2α+sin2β=2sin(α+β)cos(α-β)=-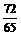
sin2α-sin2β=2cos(α+β)sin(α-β)=-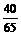
∴sin2α=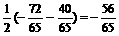
[例6]
不查表求sin220°+cos280°+ cos20°cos80°的值.
cos20°cos80°的值.
解法一:sin220°+cos280°+ sin220°cos80°
sin220°cos80°
= (1-cos40°)+
(1-cos40°)+ (1+cos160°)+
(1+cos160°)+  sin20°cos80°
sin20°cos80°
=1- cos40°+
cos40°+ cos160°+
cos160°+ sin20°cos(60°+20°)
sin20°cos(60°+20°)
=1- cos40°+
cos40°+ (cos120°cos40°-sin120°sin40°)
(cos120°cos40°-sin120°sin40°)
+ sin20°(cos60°cos20°-sin60°sin20°)
sin20°(cos60°cos20°-sin60°sin20°)
=1- cos40°-
cos40°-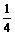 cos40°-
cos40°-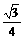 sin40°+
sin40°+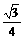 sin40°-
sin40°-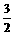 sin220°
sin220°
=1-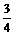 cos40°-
cos40°-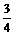 (1-cos40°)=
(1-cos40°)=
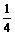
解法二:设x=sin220°+cos280°+ sin20°cos80°
sin20°cos80°
y=cos220°+sin280°- cos20°sin80°,则
cos20°sin80°,则
x+y=1+1- sin60°=
sin60°= ,x-y=-cos40°+cos160°+
,x-y=-cos40°+cos160°+ sin100°
sin100°
=-2sin100°sin60°+ sin100°=0
sin100°=0
∴x=y=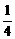 ,即x=sin220°+cos280°+
,即x=sin220°+cos280°+ sin20°cos80°=
sin20°cos80°=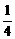 .
.
[例7]
设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a),试确定满足f(a)=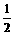 的a值,并对此时的a值求y的最大值.
的a值,并对此时的a值求y的最大值.
解:由y=2(cosx-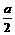 )2-
)2-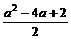 及cosx∈[-1,1]得:
及cosx∈[-1,1]得:
f(a)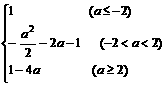
∵f(a)= ,∴1-4a=
,∴1-4a=
 a=
a=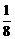
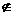 [2,+∞
[2,+∞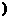
故-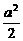 -2a-1=
-2a-1= ,解得:a=-1,此时,
,解得:a=-1,此时,
y=2(cosx+ )2+
)2+ ,当cosx=1时,即x=2kπ,k∈Z,ymax=5.
,当cosx=1时,即x=2kπ,k∈Z,ymax=5.
[例8]
求值: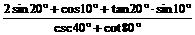 .
.
解:原式的分子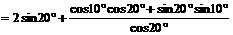
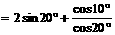
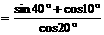
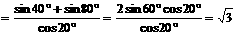 ,
,
原式的分母=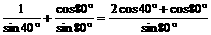
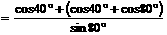
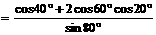
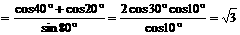 ,
,
所以,原式=1.
[例9]
已知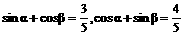 ,求
,求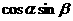 的值.
的值.
解1:令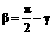 ,则原题等价于:
,则原题等价于:
已知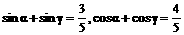 ,求
,求 的值.
的值.
两式分别和差化积并相除得: ,所以
,所以
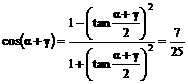 .
.
分别将已知两式平方并求和得: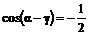 ,
,
所以,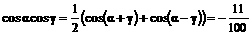 .
.
解2:由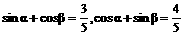 平方相加得:
平方相加得: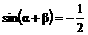 .
.
上述两式平方相减得: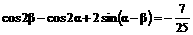 .
.
将上式前两项和差化积,得: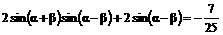 ,
,
结合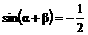 ,可解得:
,可解得: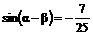 .
.
所以,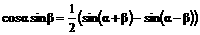
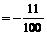 .
.
[例10]
已知函数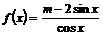 在区间
在区间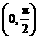 上单调递减,试求实数
上单调递减,试求实数 的取值范围.
的取值范围.
解:已知条件实际上给出了一个在区间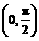 上恒成立的不等式.
上恒成立的不等式.
任取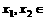
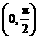 ,且
,且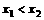 ,则不等式
,则不等式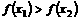 恒成立,
恒成立,
即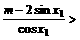
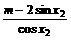 恒成立.
恒成立.
化简得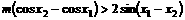
由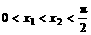 可知:
可知: ,
,
所以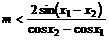
上式恒成立的条件为: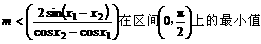 .
.
由于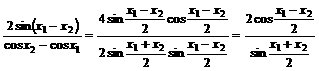
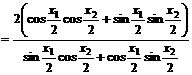
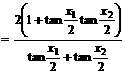
且当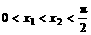 时,
时,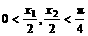 ,所以
,所以 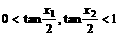 ,
,
从而 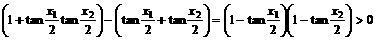 ,
,
有 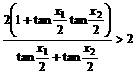 ,
,
故 的取值范围为
的取值范围为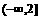 .
.
[例11]
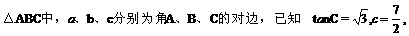
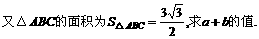
解:∵ A+B+C=π,
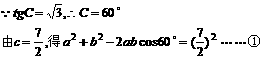
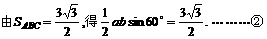
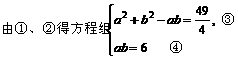
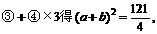

[例12]
在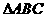 中,
中,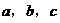 分别是角
分别是角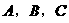 的对边,设
的对边,设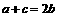 ,求
,求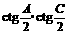 的值
的值
解:由条件,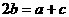 ,依据正弦定理,得
,依据正弦定理,得
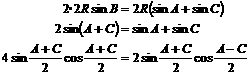
在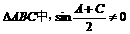
∴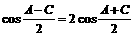
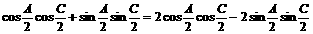
∴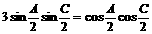
∴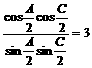 ; 即
; 即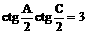
三角函数的图象与性质
[例1] 试确定下列函数的定义域
⑴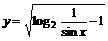 ;⑵
;⑵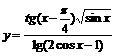
解:⑴要使函数有意义,只须满足条件
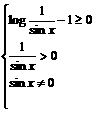 解得:
解得: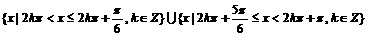
⑵要使函数有意义,只须满足条件
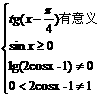 解得
解得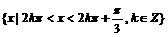
[例2]
求函数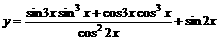 的最小值
的最小值
解:∵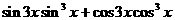
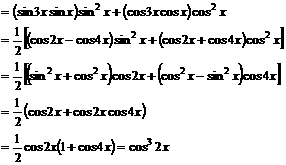
∴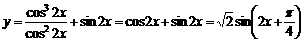
当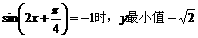
[例3]
已知函数f(x)=2asin2x-2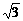 asinxcosx+a+b-1,(a、b为常数,a<0),它的定义域为[0,
asinxcosx+a+b-1,(a、b为常数,a<0),它的定义域为[0,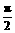 ],值域为[-3,1],试求a、b的值。
],值域为[-3,1],试求a、b的值。
解:f(x)=2asin2x-2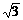 asinxcosx+a+b-1
asinxcosx+a+b-1
=a(1-cos2x)-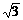 asin2x+a+b-1
asin2x+a+b-1
=-2asin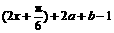
∵0≤x≤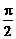 ∴
∴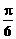 ≤2x+
≤2x+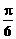 ≤
≤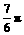 ∴
∴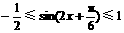
∵a<0 ∴a≤-2asin -2a
-2a
∴3a+b-1≤-2asin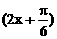 +2a+b-1≤b-1
+2a+b-1≤b-1
∵值域为[-3,1] ∴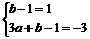 ∴
∴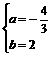
[例4]
已知函数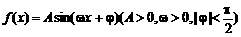 的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(
的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(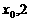 )和(
)和(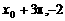 ).
).
(1)求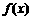 的解析式;
的解析式;
(2)将y=f(x)图象上所有点的横坐标缩短到原来的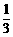 (纵坐标不变),然后再将所得图象向x轴正方向平移
(纵坐标不变),然后再将所得图象向x轴正方向平移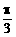 个单位,得到函数y=g(x)的图象.写出函数y=g(x)的解析式并用列表作图的方法画出y=g(x)在长度为一个周期的闭区间上的图象.
个单位,得到函数y=g(x)的图象.写出函数y=g(x)的解析式并用列表作图的方法画出y=g(x)在长度为一个周期的闭区间上的图象.
解:(1)由已知,易得A=2.
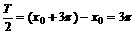 ,解得
,解得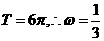 .
.
把(0,1)代入解析式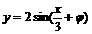 ,得
,得
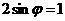 .又
.又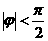 ,解得
,解得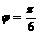 .∴
.∴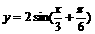 为所求.
为所求.
(2)压缩后的函数解析式为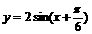 再平移,
再平移,
得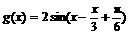
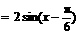
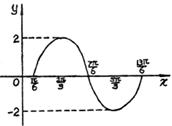
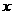
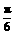
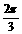
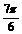
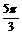
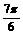
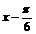
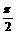

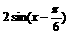
[例5]
求函数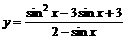 的最值,并写出使函数
的最值,并写出使函数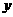 取得最值的
取得最值的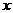 的集合。
的集合。
解:令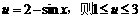 ,
,
∴函数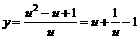
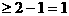
当且仅当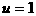 时,
时,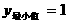
函数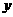 取得最小值的
取得最小值的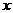 的集合
的集合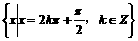
又函数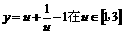 是单调递增的
是单调递增的
证明如下: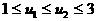
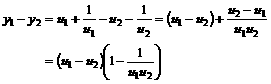
∵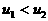 ∴
∴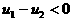
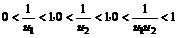
∴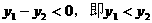 ,∴
,∴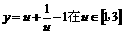 是单调递增的
是单调递增的
∴当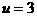 时,函数
时,函数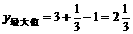
函数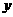 取得最大值的
取得最大值的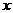 的集合
的集合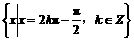
[例6]
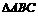 中,已知三内角A、B、C依次成等差数列,求
中,已知三内角A、B、C依次成等差数列,求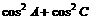 的取值范围。
的取值范围。
解:由已知得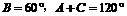
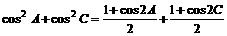
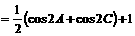
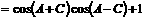
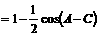
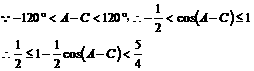
即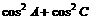 的取值范围为
的取值范围为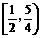
[例7]
已知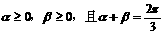 ,问当
,问当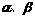 分别取何值时,
分别取何值时,
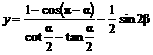 取最大值,并求出此最大值。
取最大值,并求出此最大值。
解: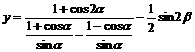
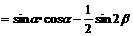
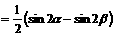
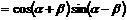
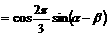
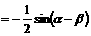
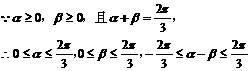
此时,由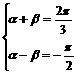 解得
解得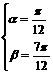
[例8]
在ΔABC中,求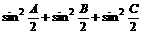 的最小值.并指出取最小值时ΔABC的形状,并说明理由.
的最小值.并指出取最小值时ΔABC的形状,并说明理由.
解:令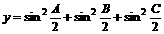
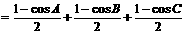
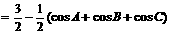
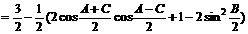
∵在ΔABC中,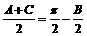 ,∴
,∴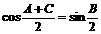
又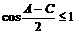 .
.
∴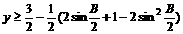
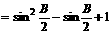
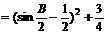
当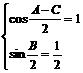 时,y取得最小值
时,y取得最小值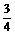 ;
;
由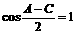 知A=C,由
知A=C,由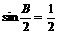 知
知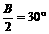 ,B=60°;
,B=60°;
故A=B=C=60°,
即y取最小值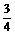 时,ΔABC的形状为等边三角形.
时,ΔABC的形状为等边三角形.
[例9]
已知函数f(x)=2cosxsin(x+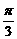 )-
)- sin2x+sinxcosx
sin2x+sinxcosx
(1)求函数f(x)的最小正周期;
(2)求f(x)的最小值及取得最小值时相应的x的值;
(3)若当x∈[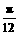 ,
,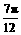 ]时,f(x)的反函数为f-1(x),求f--1(1)的值.
]时,f(x)的反函数为f-1(x),求f--1(1)的值.
解:(1)f(x)=2cosxsin(x+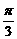 )-
)- sin2x+sinxcosx
sin2x+sinxcosx
=2cosx(sinxcos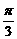 +cosxsin
+cosxsin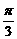 )-
)- sin2x+sinxcosx
sin2x+sinxcosx
=2sinxcosx+ cos2x=2sin(2x+
cos2x=2sin(2x+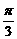 )
)
∴f(x)的最小正周期T=π
(2)当2x+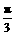 =2kπ-
=2kπ-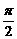 ,即x=kπ-
,即x=kπ-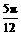 (k∈Z)时,f(x)取得最小值-2.
(k∈Z)时,f(x)取得最小值-2.
(3)令2sin(2x+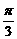 )=1,又x∈[
)=1,又x∈[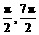 ],
],
∴2x+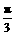 ∈[
∈[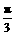 ,
,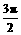 ],∴2x+
],∴2x+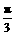 =
=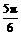 ,则
,则
x=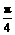 ,故f--1(1)=
,故f--1(1)=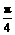 .
.
[例10]
已知α、β为锐角,且x(α+β-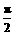 )>0,试证不等式f(x)=
)>0,试证不等式f(x)=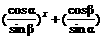 x<2对一切非零实数都成立.
x<2对一切非零实数都成立.
证明:若x>0,则α+β>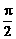 ,
,
∵α、β为锐角,∴0< -α<β<
-α<β< ;0<
;0< -β<
-β< ,
,
∴0<sin( -α)<sinβ.0<sin(
-α)<sinβ.0<sin(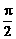 -β)<sinα,
-β)<sinα,
∴0<cosα<sinβ,0<cosβ<sinα,
∴0<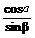 <1,0<
<1,0<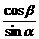 <1,
<1,
∴f(x)在(0,+∞)上单调递减,∴f(x)<f(0)=2.
若x<0,α+β< ,
,
∵α、β为锐角,0<β< -α<
-α< ,0<α<
,0<α< -β<
-β< ,0<sinβ<sin(
,0<sinβ<sin(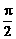 -α),
-α),
∴sinβ<cosα,0<sinα<sin( -β),∴sinα<cosβ,∴
-β),∴sinα<cosβ,∴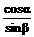 >1,
>1, 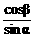 >1,
>1,
∵f(x)在(-∞,0)上单调递增,∴f(x)<f(0)=2,∴结论成立.
[例11] 设z1=m+(2-m2)i,z2=cosθ+(λ+sinθ)i,其中m,λ,θ∈R,已知z1=2z2,求λ的取值范围.
解法一:∵z1=2z2,
∴m+(2-m2)i=2cosθ+(2λ+2sinθ)i,∴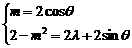
∴λ=1-2cos2θ-sinθ=2sin2θ-sinθ-1=2(sinθ-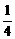 )2-
)2-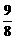 .
.
当sinθ=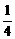 时λ取最小值-
时λ取最小值-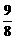 ,当sinθ=-1时,λ取最大值2.
,当sinθ=-1时,λ取最大值2.
解法二:∵z1=2z2 ∴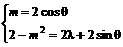
∴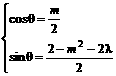 ,
,
∴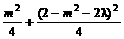 =1.
=1.
∴m4-(3-4λ)m2+4λ2-8λ=0,设t=m2,则0≤t≤4,
令f(t)=t2-(3-4λ)t+4λ2-8λ,则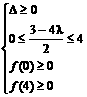 或f(0)·f(4)≤0
或f(0)·f(4)≤0
∴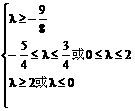
∴-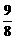 ≤λ≤0或0≤λ≤2.
≤λ≤0或0≤λ≤2.
∴λ的取值范围是[-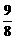 ,2].
,2].
[例12]
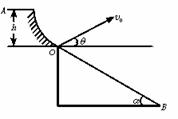 如右图,一滑雪运动员自h=50m高处A点滑至O点,由于运动员的技巧(不计阻力),在O点保持速率v0不为,并以倾角θ起跳,落至B点,令OB=L,试问,α=30°时,L的最大值为多少?当L取最大值时,θ为多大?
如右图,一滑雪运动员自h=50m高处A点滑至O点,由于运动员的技巧(不计阻力),在O点保持速率v0不为,并以倾角θ起跳,落至B点,令OB=L,试问,α=30°时,L的最大值为多少?当L取最大值时,θ为多大?
解:由已知条件列出从O点飞出后的运动方程:
|
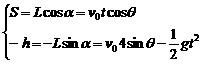
由①②整理得:v0cosθ=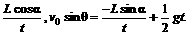
∴v02+gLsinα=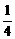 g2t2+
g2t2+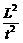 ≥
≥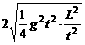 =gL
=gL
运动员从A点滑至O点,机械守恒有:mgh= mv02,
mv02,
∴v02=2gh,∴L≤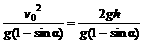 =200(m)
=200(m)
即Lmax=200(m),又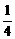 g2t2=
g2t2=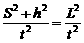 .
.
∴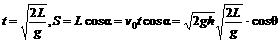
得cosθ=cosα,∴θ=α=30°∴L最大值为200米,当L最大时,起跳仰角为30°.
[例13] 如下图,某地一天从6时到14时的温度变化曲线近似满足函数:
y=Asin(ωx+φ)+b;(1)求这段时间的最大温差;(2)写出这段曲线的函数解析式.
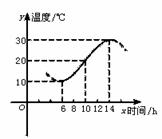
解:(1)由图示,这段时间的最大温差是30-10=20(℃);
(2)图中从6时到14时的图象是函数y=Asin(ωx+φ)+b的半个周期的图象.
∴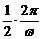 =14-6,解得ω=
=14-6,解得ω=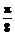 ,由图示A=
,由图示A= (30-10)=10,b=
(30-10)=10,b= (30+10)=20,这时y=10sin(
(30+10)=20,这时y=10sin(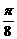 x+φ)+20,将x=6,y=10代入上式可取φ=
x+φ)+20,将x=6,y=10代入上式可取φ=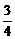 π.综上所求的解析式为y=10sin(
π.综上所求的解析式为y=10sin(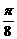 x+
x+
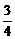 π)+20,x∈[6,14].
π)+20,x∈[6,14].
[例14]
已知函数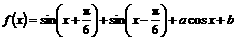 (
(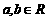 ,且均为常数),
,且均为常数),
(1)求函数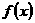 的最小正周期;
的最小正周期;
(2)若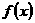 在区间
在区间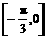 上单调递增,且恰好能够取到
上单调递增,且恰好能够取到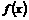 的最小值2,试求
的最小值2,试求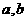 的值.
的值.
解:研究三角函数的性质(如周期、最值、单调性、奇偶性等)时,首先应该对所给的函数关系式进行化简,最好化为一个角(形如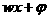 )、一种三角函数的形式.
)、一种三角函数的形式.
(1) 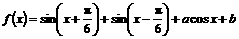
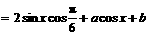
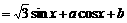
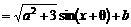
(其中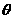 由下面的两式所确定:
由下面的两式所确定: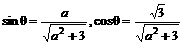 )
)
所以,函数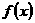 的最小正周期为
的最小正周期为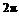 .
.
(2) 由(1)可知: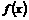 的最小值为
的最小值为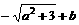 ,所以,
,所以,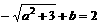 .
.
另外,由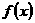 在区间
在区间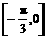 上单调递增,可知:
上单调递增,可知: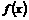 在区间
在区间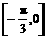 上的最小值为
上的最小值为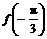 ,所以,
,所以,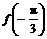 =
=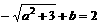 .
.
解之得: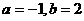
[例15]
设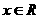 ,试比较
,试比较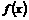 =
= 与
与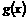 =
=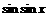 的大小关系.
的大小关系.
解:观察所给的两个函数,它们均是两个三角函数的复合函数,因此,我们不难想到:它们可能仍然具备三角函数的某些性质,如单调性、周期性、奇偶性等.
初步判断便可以确定: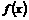 、
、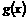 都是周期函数,且最小正周期分别为
都是周期函数,且最小正周期分别为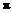 、
、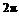 .所以,只需考虑
.所以,只需考虑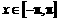 的情形.
的情形.
另外,由于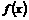 为偶函数,
为偶函数,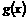 为奇函数,所以,很自然的可以联想到:能否把需考虑的
为奇函数,所以,很自然的可以联想到:能否把需考虑的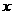 的范围继续缩小?
的范围继续缩小?
事实上,当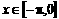 时,
时,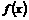 >0,
>0,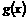
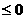 恒成立,此时,
恒成立,此时,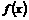 >
>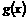 .
.
下面,我们只需考虑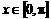 的情形.
的情形.
如果我们把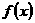 看作是关于
看作是关于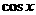 的余弦函数,把
的余弦函数,把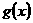 看作是关于
看作是关于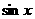 的正弦函数,那么这两个函数既不同名,自变量也不相同,为了能进行比较,我们可以作如下恒等变换,使之成为同名函数,以期利用三角函数的单调性.
的正弦函数,那么这两个函数既不同名,自变量也不相同,为了能进行比较,我们可以作如下恒等变换,使之成为同名函数,以期利用三角函数的单调性.
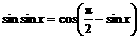
至此为止,可以看出:由于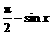 和
和 同属于余弦函数的一个单调区间,(即
同属于余弦函数的一个单调区间,(即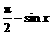 ,
,
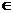
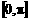 ),所以,只需比较
),所以,只需比较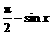 与
与 的大小即可.
的大小即可.
事实上,
(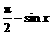 )-
)- =
=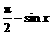 -
- =
=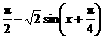
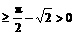
所以,利用余弦函数在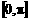 上单调递减,可得:
上单调递减,可得:
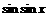 <
< .也即
.也即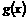 <
<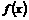
综上,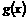 <
<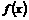 .
.
点评 本题好在充分地运用了正余弦函数的值域、周期性、奇偶性、单调性等性质,对于训练学生思维、加深对这些性质的理解、以及学习利用函数的性质去解决问题有很大的帮助.是一道很有训练价值的好题.
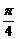 +x)=
+x)=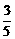 ,(
,(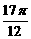 <x<
<x<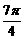 ),求
),求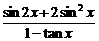 的值.
的值.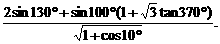
 ),β∈(0,
),β∈(0,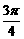 +β)=
+β)=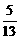 ,则sin(α+β)=_________.
,则sin(α+β)=_________.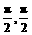 ),则tan
),则tan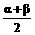 的值是( )
的值是( )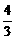 D.
D.