22. (Ⅰ) 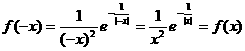
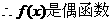 。
。
(Ⅱ)当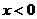 时,
时,
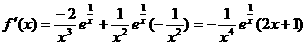
令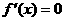 有
有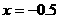 ,
,
当x变化时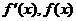 的变化情况如下表: 由表可知:
的变化情况如下表: 由表可知:
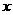 |
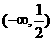 |
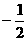 |
(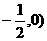 |
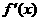 |
+ |
0 |
- |
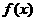 |
增 |
极大值 |
减 |
当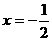 时
时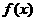 取极大值
取极大值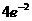 .
.
(Ⅲ)当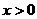 时
时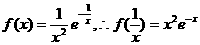
考虑到: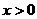 时,不等式
时,不等式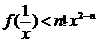 等价于
等价于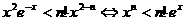 …(1)
…(1)
所以只要用数学归纳法证明不等式(1)对一切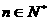 都成立即可
都成立即可
(i)当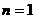 时,设
时,设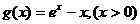
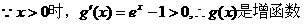 ,
,
故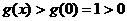 ,即
,即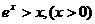
所以,当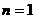 时,不等式(1)都成立
时,不等式(1)都成立
(ii)假设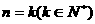 时,不等式(1)都成立,即
时,不等式(1)都成立,即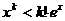
当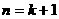 时设
时设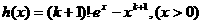
有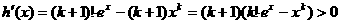
故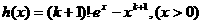 为增函数,
为增函数,
所以,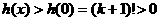 ,即
,即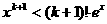 ,
,
这说明当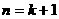 时不等式(1)也都成立,
时不等式(1)也都成立,
根据(i)(ii)可知不等式(1)对一切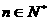 都成立,
都成立,
故原不等式对一切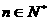 都成立.
都成立.
6 复习建议
 的展开式中,含
的展开式中,含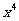 项的系数是
项的系数是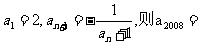
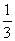 C.-
C.-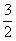 D.1
D.1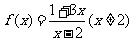 的反函数
的反函数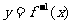 的一个单调减区间是
的一个单调减区间是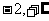 ) B.(
) B.(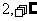 ) C.(
) C.(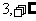 ) D.(
) D.(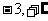 )
)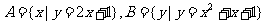 ,则
,则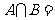
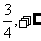 )
)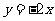 按向量
按向量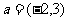 的平移后,得到的直线方程为
的平移后,得到的直线方程为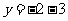 B.
B.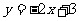
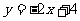 D.
D.