2. 由经验得,在某超市的付款处排队等候付款的人数及其概率如下:
|
排队人数 |
0 |
1 |
2 |
3 |
4 |
5人以上 |
|
概 率 |
0.1 |
0.16 |
0.3 |
0.3 |
0.1 |
0.04 |
求:(1)至多有2个人排队的概率;
(2)至少有2人排队的概率.
.(1)设没有人排除为事件A,1个人排队为事件B,2个人排队为事件C,则P(A)=0.1, P(B)=0.16, P(C)=0.3,依题意A、B、C彼此互斥,所以至多2个人排队的概率为:
P(A+B+C)=P(A)+P(B)+P(C)=0.1+0.16+0.3=0.56.
(2)设至少2个人排队为事件D,则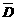 为至多1个人排队,即
为至多1个人排队,即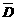 =A+B,因此
=A+B,因此
P(D)=1-P(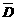 )=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
)=1-P(A+B)=1-[P(A)+P(B)]=1-(0.1+0.16)=0.74.
3用长为16米的篱笆,借助墙角围成一个矩形ABCD(如图),在P处有一棵树与两墙的距离分别为a米(0<a<12 )和4米。若此树不圈在矩形外,求矩形ABCD面积的最大值M.
解:设AB=x,则AD=16-x
,依题意得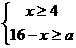 ,即
,即 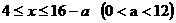
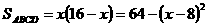
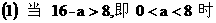 ,
,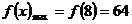
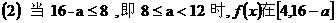 上是增函数,
上是增函数,
所以 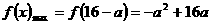 ,故
,故 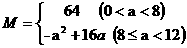
4. 已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位小时)的函数,记作y=f(t),下表是某日各时的浪高数据
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
1. 5 |
1. 0 |
0. 5 |
1. 0 |
1.49 |
1 |
0. 51 |
0.99 |
1.5 |
经长期观测y=f(t)的曲线可近似地看成函数y=Acosωt+b.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T,振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8 00至晚上20
00至晚上20 00之间,有多少时间可供冲浪者进行运动.
00之间,有多少时间可供冲浪者进行运动.
4解 (1)由表中数据,知T=12,ω=
(1)由表中数据,知T=12,ω=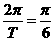 . 由t=0,y=1. 5得A+b=1. 5.
. 由t=0,y=1. 5得A+b=1. 5.
由t=3,y=1. 0,得b=1. 0. 所以,A=0. 5,b=1. 振幅A=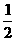 ,∴y=
,∴y=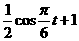
(2)由题意知,当y>1时,才可对冲浪者开放. ∴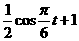 >1,
>1, 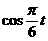 >0. ∴2kπ-
>0. ∴2kπ-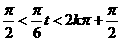 ,即有12k–3<t<13k+3. 由0≤t≤24,故可令k=0,1,2,得0≤t<3或9<t<15或21<t≤24. ∴在规定时间内有6个小时可供冲浪者运动即上午9
,即有12k–3<t<13k+3. 由0≤t≤24,故可令k=0,1,2,得0≤t<3或9<t<15或21<t≤24. ∴在规定时间内有6个小时可供冲浪者运动即上午9 00至下午15
00至下午15 00.
00.
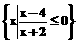 ,集合B=
,集合B=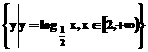 ,则
,则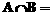 ______________.
______________.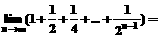 ___________.
___________. 
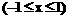 ,则
,则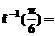 __________.
__________.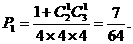
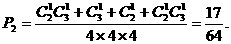
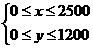 ,
,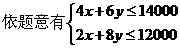 ,
,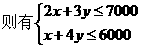 ,设利润S=1000x+2000y=1000(x+2y),要使利润S最大,只需求x+2y的最大值,
x+2y=m(2x+3y)+n(x+4y)=x(2m+n)+y(3m+4n)
,设利润S=1000x+2000y=1000(x+2y),要使利润S最大,只需求x+2y的最大值,
x+2y=m(2x+3y)+n(x+4y)=x(2m+n)+y(3m+4n)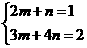 , ∴
, ∴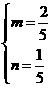 ,有x+2y=
,有x+2y=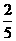 (2x+3y)+
(2x+3y)+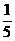 (x+4y)≤
(x+4y)≤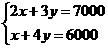 解得
解得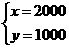 时取等号,此时最大利润Smax=1000(x+2y)=4000000=400(万元).
时取等号,此时最大利润Smax=1000(x+2y)=4000000=400(万元). 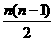 ×4]–72=–2n2+40n–72
×4]–72=–2n2+40n–72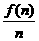 =40–2(n+
=40–2(n+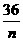 )≤16. 当且仅当n=6时取等号. 故此方案先获利6×16+48=144(万美元),此时n=6,②f(n)=–2(n–10)2+128.
)≤16. 当且仅当n=6时取等号. 故此方案先获利6×16+48=144(万美元),此时n=6,②f(n)=–2(n–10)2+128. 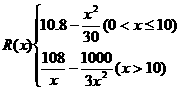 (1)写出年利润W(万元)关于年产量x(千件)的函数解析式;(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大? (注:年利润=年销售收入-年总成本)
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获利润最大? (注:年利润=年销售收入-年总成本)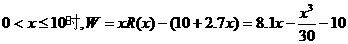
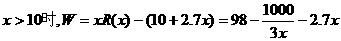
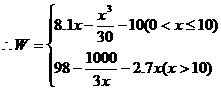
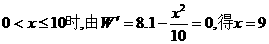
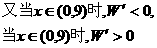
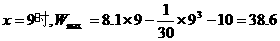
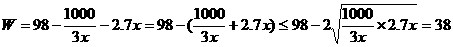
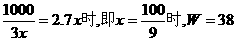
 ,去室内锻炼的人为
,去室内锻炼的人为 ,则有:
,则有: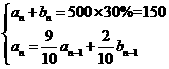 ,
,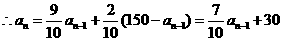 ,
,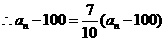 ,
,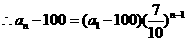 ,
,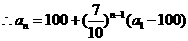 ∴
∴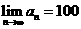 ,
,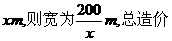
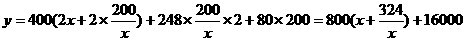 .
. 即函数定义域为[12.5,16]
即函数定义域为[12.5,16]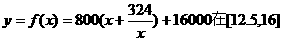 上的单调性,
上的单调性,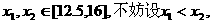
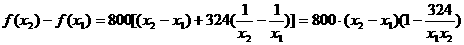
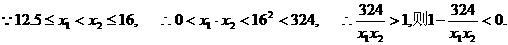
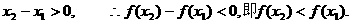
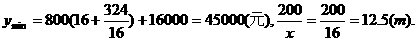
 ,墙高为
,墙高为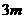 的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元
的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元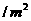 ,其余三面的造价为200元
,其余三面的造价为200元 ,则另一边的长为
,则另一边的长为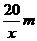 ,设总造价为
,设总造价为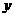 元,则
元,则
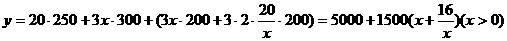
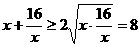 ,当且仅当
,当且仅当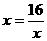 (
(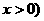 即
即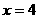 时 取“=”,所以,当
时 取“=”,所以,当 此时
此时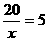 ,
, ,另一边的长为
,另一边的长为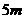 时,能使总造价最低造价为17000元。
时,能使总造价最低造价为17000元。