0 52247 52255 52261 52265 52271 52273 52277 52283 52285 52291 52297 52301 52303 52307 52313 52315 52321 52325 52327 52331 52333 52337 52339 52341 52342 52343 52345 52346 52347 52349 52351 52355 52357 52361 52363 52367 52373 52375 52381 52385 52387 52391 52397 52403 52405 52411 52415 52417 52423 52427 52433 52441 447348
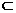 β, 则α⊥β D.若m∥α, α
∩β=n则m∥n
β, 则α⊥β D.若m∥α, α
∩β=n则m∥n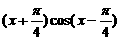 和直线在y=
和直线在y=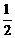 在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于
在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则|P2P4|等于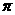 B.2
B.2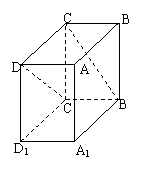 在长方体ABCD-A1B1C1D1中,B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成的角的余弦值为
在长方体ABCD-A1B1C1D1中,B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成的角的余弦值为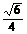 B.
B.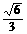
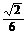 D.
D.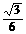
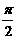 D.钝角
D.钝角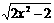 (x≤-1)反函数是
(x≤-1)反函数是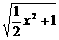 (x≥0) B.y=
(x≥0) B.y=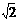 ) D.y=
) D.y=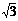 x<0},Q={x|
x<0},Q={x|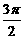 },则P∩Q=
},则P∩Q=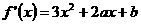 。
。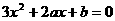 的两个根,由韦达定理得
的两个根,由韦达定理得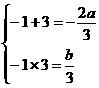
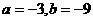
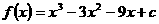
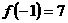 ,∴
,∴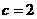
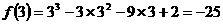
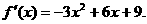 令
令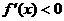 ,解得
,解得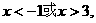
 的单调递减区间为
的单调递减区间为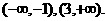
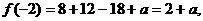
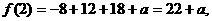
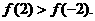 因为在(-1,3)上
因为在(-1,3)上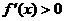 ,所以
,所以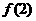 和
和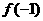 分别是
分别是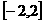 上的最大值和最小值.于是有
上的最大值和最小值.于是有 ,解得
,解得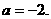
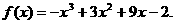 因此
因此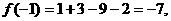
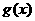 的图象都过点(
的图象都过点(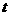 ,0),所以
,0),所以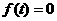 ,
,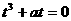 .因为
.因为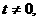 所以
所以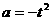 .
. 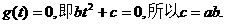
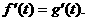
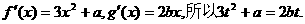
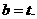 因此
因此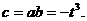 故
故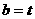 ,
,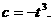
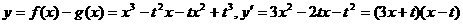 .
.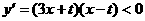 时,函数
时,函数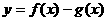 单调递减.
单调递减.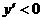 ,若
,若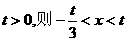 ;若
;若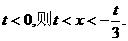
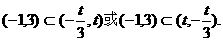 所以
所以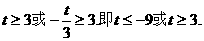
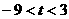 时,函数
时,函数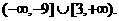
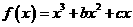 ,∴
,∴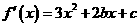 。从而
。从而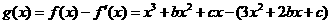 =
=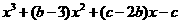 是一个奇函数,所以
是一个奇函数,所以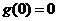 得
得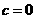 ,由奇函数定义得
,由奇函数定义得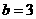 ;
;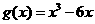 ,从而
,从而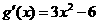 ,由此可知,
,由此可知,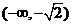 和
和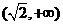 是函数
是函数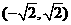 是函数
是函数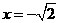 时,取得极大值,极大值为
时,取得极大值,极大值为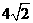 ,
,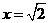 时,取得极小值,极小值为
时,取得极小值,极小值为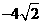 。
。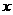 (m),则长为
(m),则长为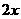 (m),高为
(m),高为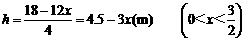 .
.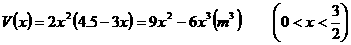
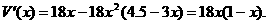
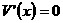 ,解得
,解得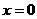 (舍去)或
(舍去)或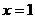 ,因此
,因此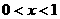 时,
时,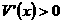 ;当
;当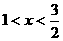 时,
时,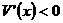 ,
,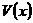 取得极大值,并且这个极大值就是
取得极大值,并且这个极大值就是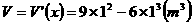 ,此时长方体的长为2 m,高为1.5 m.
,此时长方体的长为2 m,高为1.5 m.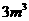 。
。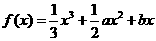 在区间
在区间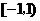 ,
,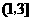 内分别有一个极值点,所以
内分别有一个极值点,所以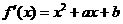
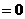 在
在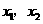 (
(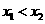 ),则
),则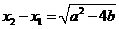 ,且
,且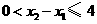 .于是
.于是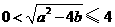 ,
,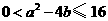 ,且当
,且当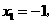
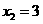 ,即
,即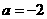 ,
,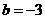 时等号成立.故
时等号成立.故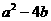 的最大值是16.
的最大值是16.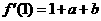 知
知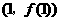 处的切线
处的切线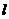 的方程是
的方程是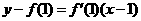 ,即
,即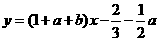 ,
,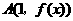 处空过
处空过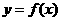 的图象,
的图象,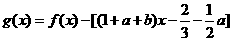 在
在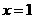 两边附近的函数值异号,则
两边附近的函数值异号,则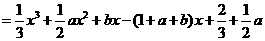 ,且
,且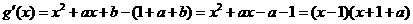 .
.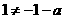 ,则
,则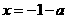 都是
都是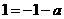 ,即
,即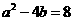 ,得
,得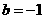 ,故
,故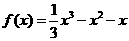 .
.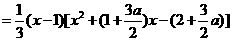 .
.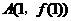 处穿过
处穿过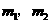 (
(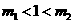 ).
).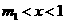 时,
时,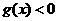 ,当
,当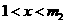 时,
时,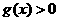 ;
;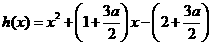 ,则
,则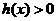 ,当
,当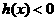 ,当
,当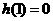 知
知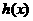 的一个极值点,则
的一个极值点,则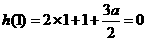 ,
,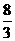 14.
14. 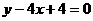 15. 7 16. 20
15. 7 16. 20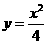 的一条切线的斜率为
的一条切线的斜率为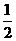 ,则切点的横坐标为(
A )
,则切点的横坐标为(
A )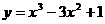 在点(1,-1)处的切线方程为 ( B )
在点(1,-1)处的切线方程为 ( B )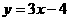 B.
B.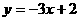 C.
C.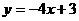 D.
D.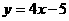
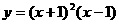 在
在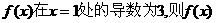 的解析式可能为 (
A )
的解析式可能为 (
A )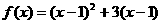 B.
B.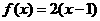
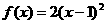 D.
D.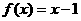
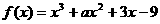 ,已知
,已知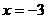 时取得极值,则
时取得极值,则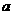 =( D )
=( D )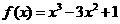 是减函数的区间为(
D )
是减函数的区间为(
D )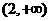 (B)
(B)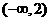 (C)
(C)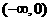 (D)
(D)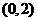
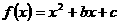 的图象的顶点在第四象限,则函数
的图象的顶点在第四象限,则函数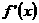 的图象是(
A )
的图象是(
A )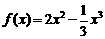 在区间
在区间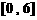 上的最大值是( A )
上的最大值是( A )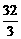 B.
B.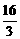 C.
C.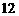 D.
D.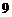
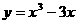 的极大值为
的极大值为 ,极小值为
,极小值为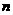 ,则
,则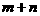 为 ( A )
为 ( A )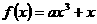 在
在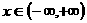 内是增函数,则 ( A )
内是增函数,则 ( A )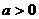 B.
B.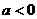 C.
C.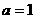 D.
D.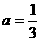
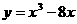 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于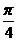 的点中,坐标为整数的点的个数是 ( D )
的点中,坐标为整数的点的个数是 ( D )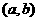 ,导函数
,导函数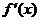 在
在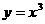 在点
在点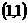 处的切线与
处的切线与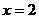 所围成的三角形的面积为__________。
所围成的三角形的面积为__________。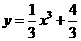 ,则过点
,则过点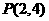 “改为在点
“改为在点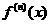 是对函数
是对函数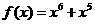 ,对于任意
,对于任意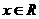 ,都有
,都有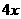 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则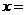 吨.
吨.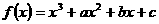 ,当
,当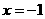 时,取得极大值7;当
时,取得极大值7;当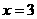 时,取得极小值.求这个极小值及
时,取得极小值.求这个极小值及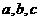 的值.
的值.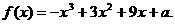
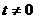 ,点P(
,点P(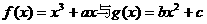 的图象的一个公共点,两函数的图象在点P处有相同的切线。
的图象的一个公共点,两函数的图象在点P处有相同的切线。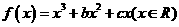 ,已知
,已知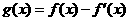 是奇函数。
是奇函数。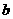 、
、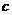 的值。
的值。 处穿过函数
处穿过函数