3.(本题满分14分)甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次为ξ;乙用这枚硬币掷2次,记正面朝上的次为η.
(1)分别求ξ和η的期望;
(2)规定;若ξ>η,则甲获胜,若ξ<η,则乙获胜,分别求出甲和乙获胜的概率.
解 ξ的可能取值为0,1,2,3则ξ的分布列为
ξ的可能取值为0,1,2,3则ξ的分布列为
|
ξ |
0 |
1 |
2 |
3 |
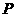 |
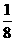 |
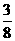 |
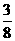 |
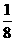 |
则Eξ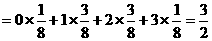
η的可能取值为0,1,2则η的分布列为
|
η |
0 |
1 |
2 |
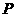 |
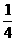 |
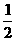 |
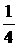 |
则Eη=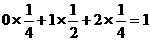
所以ξ、η的数学期望分别为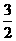 、1
、1
(2)P(ξ>η)=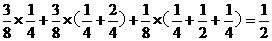
P(ξ<η)=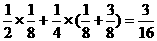
所以甲获胜的概率为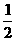 ,乙获胜的概率为
,乙获胜的概率为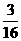 。
。
2.有3张形状、大小、质量完全相同的卡片,在各张卡片上分别标上0、1、2。现从这3张卡片中任意抽出一张,读出其标号 ,然后把这张卡片放回去,再抽一张,其标号为
,然后把这张卡片放回去,再抽一张,其标号为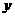 ,记
,记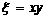 。(1)求
。(1)求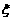 的分布列;(2)求
的分布列;(2)求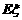 和
和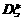 。
。
解:(1)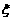 可能取的值为0、1、2、4。
……(2分)
可能取的值为0、1、2、4。
……(2分)
且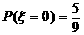 ,
,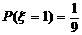 ,
,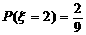 ,
,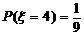 ……(6分)
……(6分)
 所求的分布列为:
所求的分布列为:
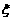 |
0 |
1 |
2 |
4 |
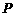 |
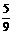 |
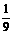 |
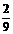 |
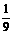 |
……(8分)
(2)由(1)可知,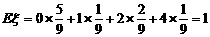 ……(11分)
……(11分)
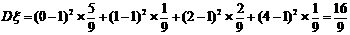 ……(14分)
……(14分)
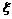
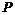
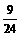
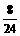
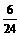
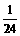
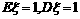 .
.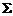 ,①求
,①求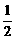 ,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=
,乙射击一次命中10环的概率为s,若他们各自独立地射击两次,设乙命中10环的次数为ξ,且ξ的数学期望Eξ=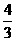 ,
,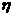 表示甲与乙命中10环的次数的差的绝对值.
表示甲与乙命中10环的次数的差的绝对值.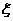 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且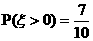 .(I) 求文娱队的人数;(II) 写出
.(I) 求文娱队的人数;(II) 写出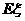 .
.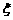 的概率分布及数学期望,
的概率分布及数学期望,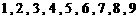 的九张卡片中,任意抽取两张,计算:
的九张卡片中,任意抽取两张,计算: