本章内容相对独立性较强,并且密切联系实际应用性较强,分为四个部分:排列组合、二项式定理、概率和概率统计。具有概念性强灵活性强,思维方法新颖等特点,要注意从加深对概念的理解和掌握内在联系与区别方面下功夫,四部分中,排列、组合是基础和工具。
本章主要的数学思想有:化归思想,比较分类思想,极限思想和模型化思维方法。学习时应注意发散思维和逆向思维,通过分类分步把复杂问题分解恰当地应用集合观点、整体思想,从全集、补集等入手,使问题简化。
[例题]
[例1] 四名优等生保送到三所学校去,每所学校至少得一名,则不同的保送方案的总数是_________.
解法一:分两步:先将四名优等生分成2,1,1三组,共有C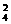 种;而后,对三组学生安排三所学校,即进行全排列,有A33种.依乘法原理,共有N=C
种;而后,对三组学生安排三所学校,即进行全排列,有A33种.依乘法原理,共有N=C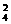
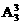 =36(种).
=36(种).
解法二:分两步:从每个学校至少有一名学生,每人进一所学校,共有A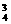 种;而后,再将剩余的一名学生送到三所学校中的一所学校,有3种.值得注意的是:同在一所学校的两名学生是不考虑进入的前后顺序的.因此,共有N=
种;而后,再将剩余的一名学生送到三所学校中的一所学校,有3种.值得注意的是:同在一所学校的两名学生是不考虑进入的前后顺序的.因此,共有N=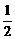 A
A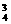 ·3=36(种).
·3=36(种).
答案:36
[例2] 有五张卡片,它们的正、反面分别写0与1,2与3,4与5,6与7,8与9,将其中任意三张并排放在一起组成三位数,共可组成多少个不同的三位数?
解:(间接法):任取三张卡片可以组成不同三位数C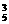 ·23·A
·23·A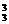 (个),其中0在百位的有C
(个),其中0在百位的有C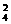 ·22·A
·22·A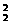 (个),这是不合题意的,故共有不同三位数:C
(个),这是不合题意的,故共有不同三位数:C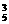 ·23·A
·23·A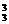 -C
-C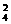 ·22·A
·22·A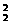 =432(个).
=432(个).
[例3] 在∠AOB的OA边上取m个点,在OB边上取n个点(均除O点外),连同O点共m+n+1个点,现任取其中三个点为顶点作三角形,可作的三角形有( )

解法一:第一类办法:从OA边上(不包括O)中任取一点与从OB边上(不包括O)中任取两点,可构造一个三角形,有C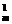 C
C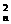 个;第二类办法:从OA边上(不包括O)中任取两点与OB边上(不包括O)中任取一点,与O点可构造一个三角形,有C
个;第二类办法:从OA边上(不包括O)中任取两点与OB边上(不包括O)中任取一点,与O点可构造一个三角形,有C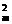 C
C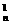 个;第三类办法:从OA边上(不包括O)任取一点与OB边上(不包括O)中任取一点,与O点可构造一个三角形,有C
个;第三类办法:从OA边上(不包括O)任取一点与OB边上(不包括O)中任取一点,与O点可构造一个三角形,有C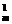 C
C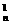 个.由加法原理共有N=C
个.由加法原理共有N=C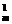 C
C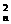 +C
+C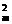 C
C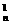 +C
+C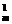 C
C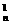 个三角形.
个三角形.
解法二:从m+n+1中任取三点共有C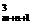 个,其中三点均在射线OA(包括O点),有C
个,其中三点均在射线OA(包括O点),有C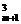 个,三点均在射线OB(包括O点),有C
个,三点均在射线OB(包括O点),有C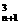 个.所以,个数为N=C
个.所以,个数为N=C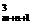 -C
-C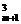 -C
-C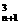 个.
个.
答案:C
[例4]
函数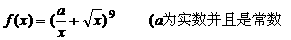 )
)
(1)已知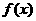 的展开式中
的展开式中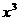 的系数为
的系数为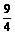 ,求常数
,求常数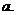
(2)是否存在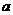 的值,使
的值,使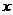 在定义域中取任意值时,
在定义域中取任意值时, 恒成立?如存在,求出
恒成立?如存在,求出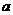 的值,如不存在,说明理由.
的值,如不存在,说明理由.
解(1)Tr+1=C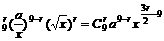 由
由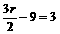 解得
解得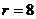
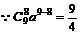
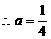
(2)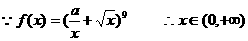 要使(
要使(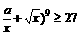
只需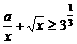
10当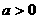 时,设
时,设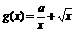
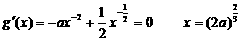
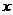 |
(0,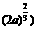 |
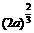 |
(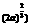 ,+ ,+ ) ) |
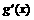 |
- |
0 |
+ |
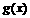 |
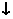 |
极小值 |
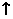 |
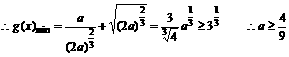
20当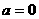 时,不成立 30当
时,不成立 30当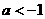 时,不成立 故当
时,不成立 故当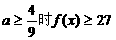
另解法
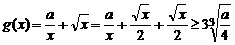 只需
只需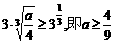
[例5] 五人站成一列,重新站队时,各人都不站在原来的位置上,有多少种站法?
解:设原来站在第i个位置的人是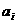 (i=1,2,3,4,5)。重新站队时,
(i=1,2,3,4,5)。重新站队时,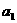 站在第2
站在第2
个位置的站法有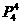 种,其中不符合要求的有:
种,其中不符合要求的有: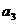 站第3位的
站第3位的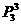 种,
种,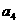 站第4位的
站第4位的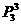 种,但有的站法在考虑
种,但有的站法在考虑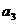 的情形时已经减去了,故只应再算(
的情形时已经减去了,故只应再算(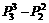 )种,同理,
)种,同理,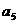 站第5位的应再算[
站第5位的应再算[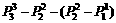 ]种。
]种。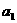 站在第3,4,5位的情形与站在第2位的情形时对等的,故所有符合要求的站法有:
站在第3,4,5位的情形与站在第2位的情形时对等的,故所有符合要求的站法有:
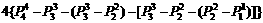 =44(种)
=44(种)
[例6] 一个口袋内装有4个不同的红球,6个不同的白球,若取出一个红球记2分,取出一个白球记1分,从口袋中取5个球,使总分不小于7分的取法有多少种?
解:设取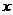 个红球,
个红球, 个白球,于是:
个白球,于是:
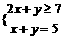 ,其中
,其中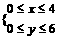 ,
,
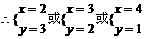
因此所求的取法种数是: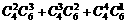 =186(种)
=186(种)
[例7]
已知数列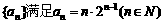 ,是否存在等差数列
,是否存在等差数列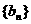 ,使
,使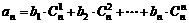 对一切自然数n都成立?并证明你的结论。
对一切自然数n都成立?并证明你的结论。
解:假设满足要求的等差数列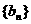 存在,由于所给等式对一切自然数n均成立,故当n=1,2,3时等式成立,从而可解得
存在,由于所给等式对一切自然数n均成立,故当n=1,2,3时等式成立,从而可解得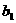 =1,
=1,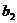 =2,
=2,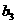 =3,因此若满足要求的等差数列存在,则必须是
=3,因此若满足要求的等差数列存在,则必须是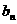 =n。.然后再证明当
=n。.然后再证明当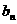 =n时所给等式确实成立即可。答案是肯定的。
=n时所给等式确实成立即可。答案是肯定的。
[例8]
若某一等差数列的首项为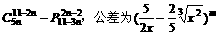 ,其中m是
,其中m是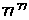 -15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
解:由已知得: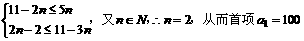 。
。
注意到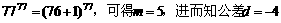 ,从而等差数列的通项公式是:
,从而等差数列的通项公式是: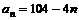 ,设其前k项之和最大,则
,设其前k项之和最大,则
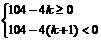 ,解得k=25或k=26,故此数列的前25项之和与前26项之和相等且最大,
,解得k=25或k=26,故此数列的前25项之和与前26项之和相等且最大,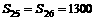 。
。
[例9]
已知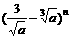 的展开式的各项系数之和等于
的展开式的各项系数之和等于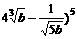 展开式中的常数项,求
展开式中的常数项,求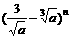 展开式中含
展开式中含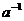 的项的二项式系数。
的项的二项式系数。
解:先求出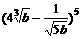 的常数项是27,从而可得
的常数项是27,从而可得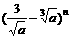 中n=7,对于
中n=7,对于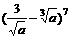 由二项展开式的通项公式知,含
由二项展开式的通项公式知,含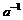 的项是第4项,其二项式系数是35。
的项是第4项,其二项式系数是35。
[例10]
求证: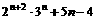 能被25整除。
能被25整除。
解:注意到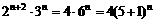 即可。
即可。
[排列、组合与二项式定理练习1]