0 52295 52303 52309 52313 52319 52321 52325 52331 52333 52339 52345 52349 52351 52355 52361 52363 52369 52373 52375 52379 52381 52385 52387 52389 52390 52391 52393 52394 52395 52397 52399 52403 52405 52409 52411 52415 52421 52423 52429 52433 52435 52439 52445 52451 52453 52459 52463 52465 52471 52475 52481 52489 447348
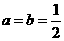 ,c=π,则对任意的x∈R,af(x)+bf(x−c)=1,由此得
,c=π,则对任意的x∈R,af(x)+bf(x−c)=1,由此得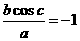 。选C。
。选C。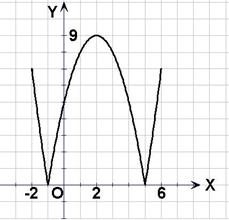 17解:(1)
17解:(1)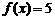 的解分别是
的解分别是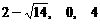 和
和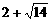 ,由于
,由于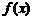 在
在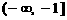 和
和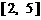 上单调递减,在
上单调递减,在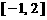 和
和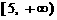 上单调递增,因此
上单调递增,因此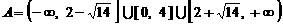 .
. 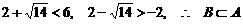 .
. 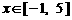 时,
时,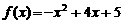 .
.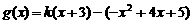
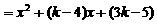
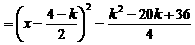 ,
, 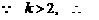
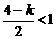 . 又
. 又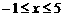 ,
,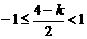 ,即
,即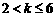 时,取
时,取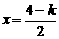 ,
,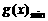
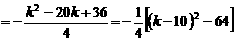 .
.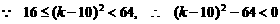 ,
, .
. 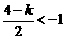 ,即
,即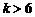 时,取
时,取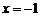 ,
, 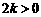 .
.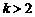 时,
时,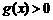 ,
,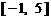 上,
上,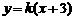 的图像位于函数
的图像位于函数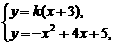 得
得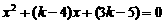 ,
,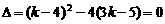 ,解得
,解得 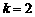 或
或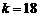 ,
, 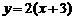 的图像与函数
的图像与函数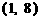 ; 当
; 当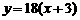 的图像与函数
的图像与函数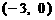 ,当
,当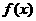 是奇函数,所以
是奇函数,所以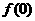 =0,即
=0,即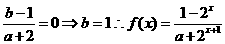
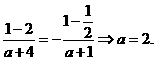
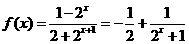 ,易知
,易知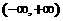 上
上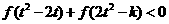
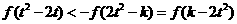 ,因
,因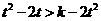 .即对一切
.即对一切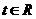 有:
有: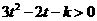 ,
,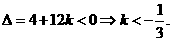
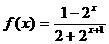 .又由题设条件得:
.又由题设条件得: 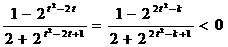 ,
,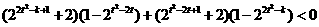 ,
,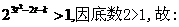
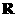 ,
,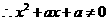 恒成立,
恒成立,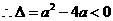 ,
,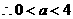 ,即当
,即当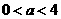 时
时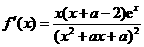 ,令
,令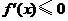 ,得
,得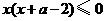 .
.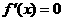 ,得
,得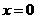 或
或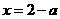 ,又
,又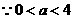 ,
,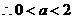 时,由
时,由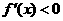 得
得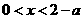 ;
;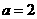 时,
时,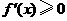 ;当
;当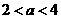 时,由
时,由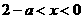 ,
,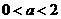 时,
时,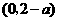 ;
;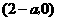 .
.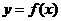 与
与 在公共点
在公共点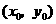 处的切线相同.
处的切线相同.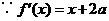 ,
,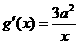 ,由题意
,由题意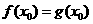 ,
,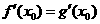 .
.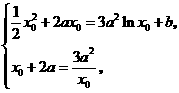 由
由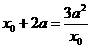 得:
得: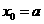 ,或
,或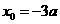 (舍去).
(舍去).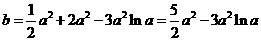 .
.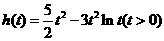 ,则
,则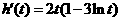 .于是
.于是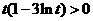 ,即
,即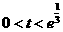 时,
时,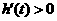 ;
; ,即
,即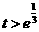 时,
时,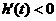 .
.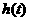 在
在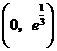 为增函数,在
为增函数,在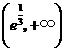 为减函数,
为减函数,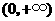 的最大值为
的最大值为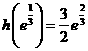 .
.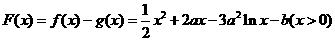 ,
,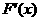
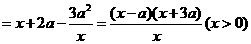 .
.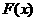 在
在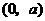 为减函数,在
为减函数,在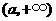 为增函数,
为增函数,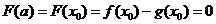 .
.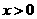 时,有
时,有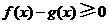 ,即当
,即当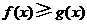 .
.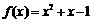 ,
,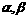 是方程f(x)=0的两个根
是方程f(x)=0的两个根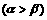 ,
,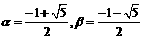 ;
;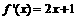 ,
,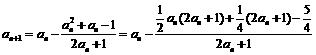
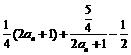 ,∵
,∵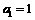 ,∴有基本不等式可知
,∴有基本不等式可知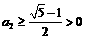 (当且仅当
(当且仅当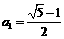 时取等号),∴
时取等号),∴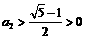 同,样
同,样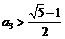 ,……,
,……,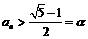 (n=1,2,……),
(n=1,2,……),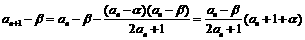 ,而
,而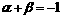 ,即
,即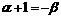 ,
,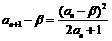 ,同理
,同理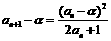 ,
,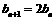 ,又
,又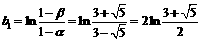
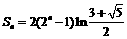
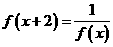 得
得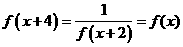 ,所以
,所以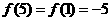 ,则
,则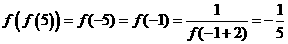 。
。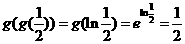 .
.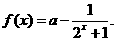 若
若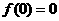 ,即
,即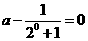 ,a=
,a=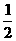 .
.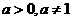 ,函数
,函数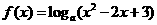 有最小值可知a>1,所以不等式
有最小值可知a>1,所以不等式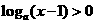 可化为x-1>1,即x>2.
可化为x-1>1,即x>2.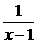 >1.
>1.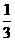 ,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³
,又当x<1时,(3a-1)x+4a>7a-1,当x>1时,logax<0,所以7a-1³0解得x³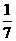 故选C
故选C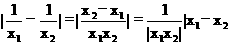 |
|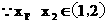
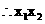 >1
>1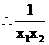 <1\
<1\ 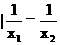 |<|x1-x2|故选A
|<|x1-x2|故选A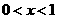 时,
时,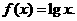 设
设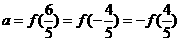 ,
,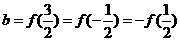 ,
,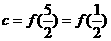 <0,∴
<0,∴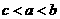 ,选D.
,选D.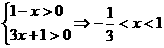 ,故选B.
,故选B.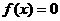 的根是
的根是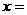 2,故选C
2,故选C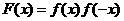 则
则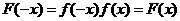 ,
,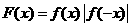 ,
,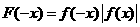 此时
此时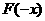 的关系不能确定,即函数
的关系不能确定,即函数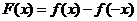 ,
,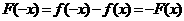 ,即函数
,即函数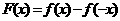 为奇函数,D中
为奇函数,D中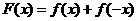 ,
,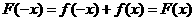 ,即函数
,即函数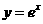 的图象与函数
的图象与函数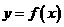 的图象关于直线
的图象关于直线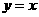 对称,所以
对称,所以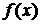 是
是 ,∴
,∴ 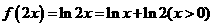 ,选D.
,选D.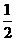 时,|x+1|=x+1,|x-2|=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当
时,|x+1|=x+1,|x-2|=2-x,因为(x+1)-(2-x)=2x-1<0,x+1<2-x;当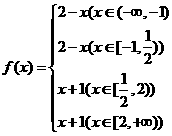 据此求得最小值为
据此求得最小值为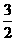 。选C
。选C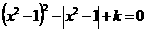 可化为
可化为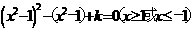 …(1)
…(1)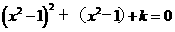 (-1<x<1)…………(2)
(-1<x<1)…………(2)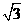 ,方程(2)无解,原方程恰有2个不同的实根
,方程(2)无解,原方程恰有2个不同的实根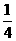 时,方程(1)有两个不同的实根±
时,方程(1)有两个不同的实根±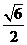 ,方程(2)有两个不同的实根±
,方程(2)有两个不同的实根±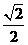 ,即原方程恰有4个不同的实根
,即原方程恰有4个不同的实根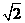 ,方程(2)的解为x=0,原方程恰有5个不同的实根
,方程(2)的解为x=0,原方程恰有5个不同的实根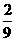 时,方程(1)的解为±
时,方程(1)的解为±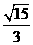 ,±
,±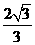 ,方程(2)的解为±
,方程(2)的解为±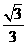 ,±
,±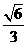 ,即原方程恰有8个不同的实根
,即原方程恰有8个不同的实根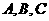 的机动车辆数如图所示,图中
的机动车辆数如图所示,图中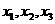 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段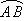 、
、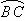 、
、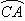 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则 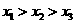 (B)
(B)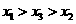 (C)
(C)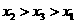 (D)
(D)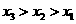
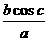 的值等于( )
的值等于( )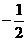 B.
B. 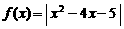 .
.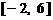 上画出函数
上画出函数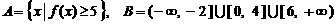 . 试判断集合
. 试判断集合 和
和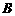 之间的关系,并给出证明;
之间的关系,并给出证明;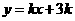 的图像位于函数
的图像位于函数 的函数
的函数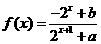 是奇函数。
是奇函数。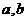 的值;
的值;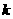 的取值范围;
的取值范围;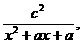 其中a为实数.
其中a为实数.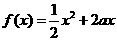 ,
,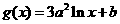 ,其中
,其中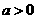 .设两曲线
.设两曲线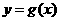 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.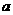 表示
表示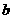 ,并求
,并求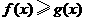 (
(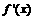 是f(x)的导数;设
是f(x)的导数;设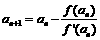 (n=1,2,……)
(n=1,2,……)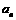 >a;
>a;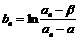 (n=1,2,……),求数列{bn}的前n项和Sn。
(n=1,2,……),求数列{bn}的前n项和Sn。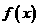 对于任意实数
对于任意实数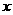 满足条件
满足条件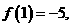 则
则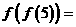 _______________。
_______________。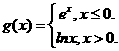 则
则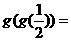 __________
__________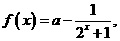 ,若
,若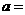 ________。
________。