0 51489 51497 51503 51507 51513 51515 51519 51525 51527 51533 51539 51543 51545 51549 51555 51557 51563 51567 51569 51573 51575 51579 51581 51583 51584 51585 51587 51588 51589 51591 51593 51597 51599 51603 51605 51609 51615 51617 51623 51627 51629 51633 51639 51645 51647 51653 51657 51659 51665 51669 51675 51683 447348
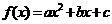 ;顶点式:
;顶点式: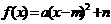 ;零点式:
;零点式: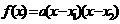 ,要会根据已知条件的特点,灵活地选用二次函数的表达形式)。
,要会根据已知条件的特点,灵活地选用二次函数的表达形式)。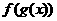 的表达式,求
的表达式,求 的表达式。这里需值得注意的是所求解析式的定义域的等价性,即
的表达式。这里需值得注意的是所求解析式的定义域的等价性,即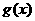 的值域。
的值域。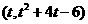 ,则
,则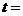
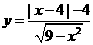 的奇偶性____(3)判断
的奇偶性____(3)判断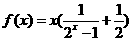 的奇偶性___.
的奇偶性___.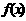 在
在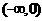 上是减函数,且
上是减函数,且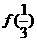 =2,则不等式
=2,则不等式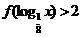 的解集为
的解集为
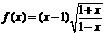 的奇偶性
(6)判断下列函数
的奇偶性
(6)判断下列函数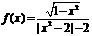 奇偶性
奇偶性 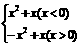 的奇偶性: (8)若
的奇偶性: (8)若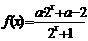 为奇函数,则实数
为奇函数,则实数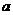 =
=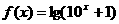 ,表示成一个奇函数
,表示成一个奇函数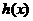 之和,则
之和,则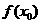 时,一定首先要判断
时,一定首先要判断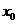 属于定义域的哪个子集,然后再代相应的关系式;分段函数的值域应是其定义域内不同子集上各关系式的取值范围的并集。
属于定义域的哪个子集,然后再代相应的关系式;分段函数的值域应是其定义域内不同子集上各关系式的取值范围的并集。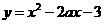 在区间[1, 2]上存在反函数的充要条件是
在区间[1, 2]上存在反函数的充要条件是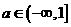 B、
B、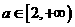 C、
C、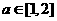 D、
D、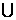
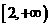
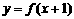 的反函数不是
的反函数不是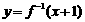 ,而是
。
,而是
。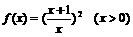 .求
.求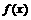 的反函数
的反函数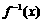
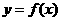 的图象过点(1,1),那么
的图象过点(1,1),那么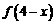 的反函数的图象一定经过点____
的反函数的图象一定经过点____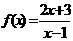 ,若函数
,若函数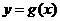 与
与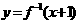 的图象关于直线
的图象关于直线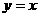 对称,求
对称,求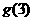 的值
的值
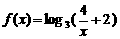 ,则方程
,则方程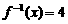 的解
的解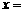 ______;
______;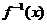 ,f (4)=0,则
,f (4)=0,则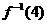 =
= 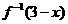 的图象一定经过
的图象一定经过 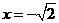 ,截
,截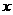 轴上的弦长为
轴上的弦长为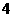 ,且过点
,且过点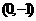 ,求函数的解析式
.
,求函数的解析式
.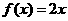 的解分别是-1,3,若方程
的解分别是-1,3,若方程 有两个相等的实数根,求
有两个相等的实数根,求 求
求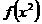 的解析式
;
的解析式
;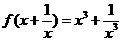 ,求
,求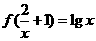 ,求
,求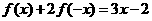 ,求
,求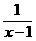 ,则
,则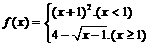 ,则使得
,则使得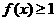 的自变量
的自变量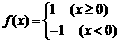 ,则不等式
,则不等式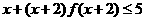 的解集是________
的解集是________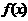 ,满足
,满足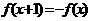 ,当
,当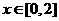
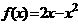 。求函数
。求函数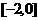 上的解析式
上的解析式
 是偶函数,
是偶函数,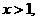
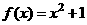 。求
。求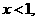
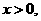
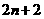 个3. 9;4.(1)
个3. 9;4.(1)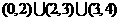 ;
;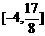 (2)
(2)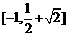
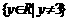 .(5)
.(5)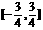 。(6)
。(6)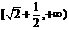 。(7){y| y>1 或y
。(7){y| y>1 或y
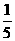 且y
且y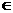 R}.
R}.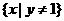 (9)
(9)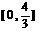 .(10)
.(10)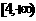 (11)
(11)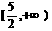 。(12){y| y
。(12){y| y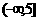 .(14)
.(14)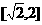 。
。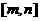 上的最值;二是求区间定(动),对称轴动(定)的最值问题。求二次函数的最值问题,勿忘数形结合,注意“两看”:一看开口方向;二看对称轴与所给区间的相对位置关系),
上的最值;二是求区间定(动),对称轴动(定)的最值问题。求二次函数的最值问题,勿忘数形结合,注意“两看”:一看开口方向;二看对称轴与所给区间的相对位置关系),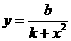 型,可直接用不等式性质,②
型,可直接用不等式性质,②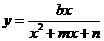 型,先化简,再用均值不等式,③
型,先化简,再用均值不等式,③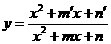 型,通常用判别式法;④
型,通常用判别式法;④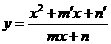 型,可用判别式法或均值不等式法,
型,可用判别式法或均值不等式法,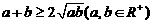 求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。
求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。 中
中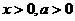 且
且 ,三角形中
,三角形中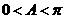 , 最大角
, 最大角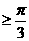 ,最小角
,最小角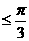 等。(2)根据实际问题的要求确定自变量的范围。
等。(2)根据实际问题的要求确定自变量的范围。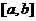 ,其复合函数
,其复合函数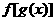 的定义域由不等式
的定义域由不等式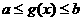 解出即可;若已知
解出即可;若已知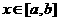 时,求
时,求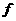 : A
: A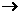 B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与
B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与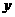 轴垂线的公共点可能没有,也可能有任意个。
轴垂线的公共点可能没有,也可能有任意个。