摘要:求函数值域的方法: (1)配方法――二次函数(二次函数在给出区间上的最值有两类:一是求闭区间上的最值,二是求区间定的最值问题.求二次函数的最值问题.勿忘数形结合.注意“两看 :一看开口方向,二看对称轴与所给区间的相对位置关系). (2)换元法――通过换元把一个较复杂的函数变为简单易求值域的函数.其函数特征是函数解析式含有根式或三角函数公式模型. (3)函数有界性法――直接求函数的值域困难时.可以利用已学过函数的有界性.来确定所求函数的值域.最常用的就是三角函数的有界性. (4)单调性法――利用一次函数.反比例函数.指数函数.对数函数等函数的单调性. (5)数形结合法――函数解析式具有明显的某种几何意义.如两点的距离.直线斜率.等等. 注意:求两点距离之和时.要将函数式变形.使两定点在轴的两侧.而求两点距离之差时.则要使两定点在轴的同侧. (6)判别式法――对分式函数(分子或分母中有一个是二次)都可通用.但这类题型有时也可以用其它方法进行求解.不必拘泥在判别式法上.也可先通过部分分式后.再利用均值不等式: ①型.可直接用不等式性质.②型.先化简.再用均值不等式.③型.通常用判别式法,④型.可用判别式法或均值不等式法. (7)不等式法――利用基本不等式求函数的最值.其题型特征解析式是和式时要求积为定值.解析式是积时要求和为定值.不过有时须要用到拆项.添项和两边平方等技巧. (8)导数法――一般适用于高次多项式函数 提醒:(1)求函数的定义域.值域时.你按要求写成集合形式了吗? (2)函数的最值与值域之间有何关系?
网址:http://m.1010jiajiao.com/timu3_id_515864[举报]
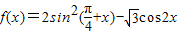 .
. 内的值域.
内的值域.
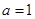 时,求函数
时,求函数 在
在 的值域;
的值域;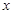 的方程
的方程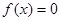 有解,求
有解,求 的取值范围.
的取值范围.