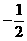例6、下表给出一个“等差数阵”:
|
4 |
7 |
( ) |
( ) |
( ) |
…… |
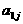 |
…… |
|
7 |
12 |
( ) |
( ) |
( ) |
…… |
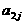 |
…… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
…… |
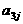 |
…… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
…… |
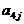 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
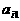 |
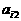 |
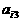 |
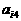 |
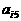 |
…… |
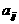 |
…… |
|
…… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
其中每行、每列都是等差数列,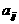 表示位于第i行第j列的数。
表示位于第i行第j列的数。
(I)写出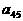 的值;(II)写出
的值;(II)写出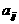 的计算公式;
的计算公式;
(III)证明:正整数N在该等差数列阵中的充要条件是2N+1可以分解成两个不是1的正整数之积。
解:(I)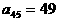 (详见第二问一般性结论)。
(详见第二问一般性结论)。
(II)该等差数阵的第一行是首项为4,公差为3的等差数列: 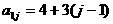 ; 第二行是首项为7,公差为5的等差数列:
; 第二行是首项为7,公差为5的等差数列: 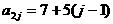 , ……,第i行是首项为
, ……,第i行是首项为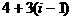 ,公差为
,公差为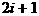 的等差数列,因此
的等差数列,因此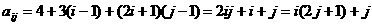
(III)必要性:若N在该等差数阵中,则存在正整数i,j使得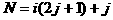 ,从而
,从而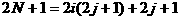
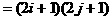 。 即正整数2N+1可以分解成两个不是1的正整数之积。
。 即正整数2N+1可以分解成两个不是1的正整数之积。
充分性:若2N+1可以分解成两个不是1的正整数之积,由于2N+1是奇数,则它必为两个不是1的奇数之积,即存在正整数k,l,使得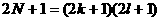 , 从而
, 从而 可见N在该等差数阵中。
可见N在该等差数阵中。
综上所述,正整数N在该等差数阵中的充要条件是2N+1可以分解成两个不是1的正整数之积。
评析: 本小题主要考查等差数列、充要条件等基本知识,考查逻辑思维能力、分析问题和解决问题的能力。求解关键是如何根据图表信息求出行列式中对应项的通项公式。
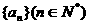 是等差数列,则有数列
是等差数列,则有数列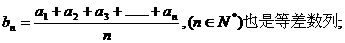 类比上述性质,相应地:若数列
类比上述性质,相应地:若数列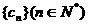 是等比数列,且
是等比数列,且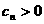 ,则有数列
,则有数列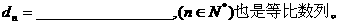
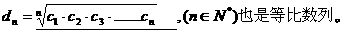
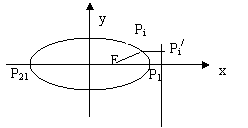 3、设F是椭圆
3、设F是椭圆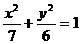 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为
.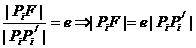 ,这些线段长度的最小值为右焦点到右顶点的距离即|FP1|=
,这些线段长度的最小值为右焦点到右顶点的距离即|FP1|=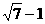 ,最大值为右焦点到左顶点的距离即|FP21|=
,最大值为右焦点到左顶点的距离即|FP21|=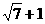 ,故若公差d>0,则
,故若公差d>0,则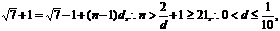 同理若公差d<0,则可求得
同理若公差d<0,则可求得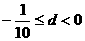 。
。 。
。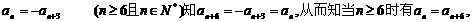 于是知
于是知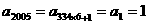 。
。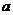 .
.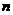 年与第
年与第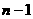 年(
年(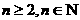 )的产量之间的关系式;
)的产量之间的关系式;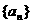 、
、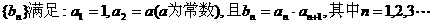
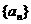 的前n项和
的前n项和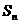 满足:
满足: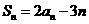 (n
(n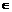 N+)。
N+)。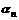 ;
;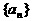 的前n项和为
的前n项和为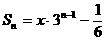 ,则x的值为
,则x的值为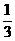 B.
B.
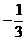 C.
C.
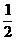 D.
D.