摘要:已知是定义在R上的函数.其图象交x轴于A.B.C三点.若点B的坐标为 (2.0).且f (x) 在[-1.0]和[4.5]上有相同的单调性.在[0.2]和[4.5]上有相反的单调性. (1)求c的值, (2)在函数f (x)的图象上是否存在一点M(x0.y0).使得f (x)在点M的切线斜率为3b?若存在.求出点M的坐标,若不存在.请说明理由, (3)求| AC |的取值范围. (1)解: 依题意在和[0.2]上有相反的单调性. ∴x = 0是f (x)的一个极值点.故.得c = 0 (2)解:因为f (x)交x轴于点B(2.0) ∴.即 令得 因为f (x)在[0.2]和[4.5]上有相反的单调性.∴在[0.2]和[4.5]上有相反的 符号 故2≤≤4 Þ -6≤≤-3 假设存在点M(x0.y0)使得f (x)在点M的切线斜率为3b.则f / (x0) =3b. 即 而-6≤≤-3.∴△<0 故不存在点M(x0.y0).使得f (x)在点M的切线斜率为3b. (3)解:设.依题意可令 则即 ∴ ∵-6≤≤-3.∴当时., 当时..故3≤| AC |≤4
网址:http://m.1010jiajiao.com/timu3_id_501426[举报]
已知![]() 是定义在R上的函数,其图象交x轴于A,B,C三点,若点B的坐标为(2,0),且
是定义在R上的函数,其图象交x轴于A,B,C三点,若点B的坐标为(2,0),且![]() 在
在![]() 和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
和[4,5]上有相同的单调性,在[0,2]和[4,5]上有相反的单调性.
(1)求c的值;
(2)在函数![]() 的图象上是否存在一点M(x0,y0),使得
的图象上是否存在一点M(x0,y0),使得![]() 在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
在点M的切线斜率为3b?若存在,求出点M的坐标;若不存在,说明理由;
已知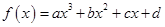 是定义在R上的函数,其图象交
是定义在R上的函数,其图象交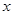 轴于A、B、C三点,若B点坐标为
轴于A、B、C三点,若B点坐标为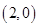 ,且
,且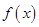 在
在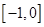 和
和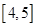 上有相同的单调性,在
上有相同的单调性,在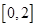 和
和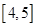 上有相反的单调性.
上有相反的单调性.
(1)求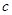 的值;
的值;
(2)在函数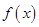 的图象上是否存在一点
的图象上是否存在一点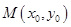 ,使得
,使得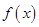 在点M的切线的斜率为
在点M的切线的斜率为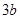 ?若存在,求出M点的坐标;若不存在,说明理由;
?若存在,求出M点的坐标;若不存在,说明理由;
(3)求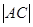 的取值范围.
的取值范围.
查看习题详情和答案>>
已知![]() 是定义在R上的函数,其图象交x轴于A、B、C三点.点B的坐标为(2,0),且
是定义在R上的函数,其图象交x轴于A、B、C三点.点B的坐标为(2,0),且![]() 的相反的单调性.
的相反的单调性.
(1)求c的值;
(2)若函数![]() 上也有反的单调性,
上也有反的单调性,![]() 的图象上是否存在一点M,使得
的图象上是否存在一点M,使得![]() 在点M的切线斜率为3b?若存在,求出M的坐标,若不存在,请说明理由.
在点M的切线斜率为3b?若存在,求出M的坐标,若不存在,请说明理由.
(3)求|AC|的取值范围.
查看习题详情和答案>>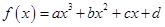 是定义在R上的函数,其图象交
是定义在R上的函数,其图象交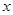 轴于A、B、C三点,若B点坐标为
轴于A、B、C三点,若B点坐标为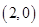 ,且
,且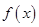 在
在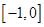 和
和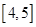 上有相同的单调性,在
上有相同的单调性,在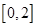 和
和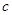 的值;
的值; ,使得
,使得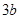 ?若存在,求出M点的坐标;若不存在,说明理由;
?若存在,求出M点的坐标;若不存在,说明理由;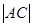 的取值范围.
的取值范围.