5.解析几何
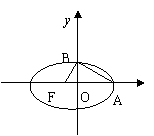 例17 如图,椭圆中心在坐标原点,F为左焦点,当
例17 如图,椭圆中心在坐标原点,F为左焦点,当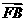 ⊥
⊥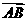 时,
时,
|
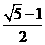 ,此类椭圆被称为“黄金椭圆”.类比黄金椭圆,
,此类椭圆被称为“黄金椭圆”.类比黄金椭圆,
可推算出“黄金双曲线”的离心率e 等于_____________ .
点通:猜想出“黄金双曲线”的离心率e 等于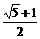 .事实上
.事实上
对直角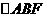 应用勾股定理,得
应用勾股定理,得 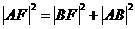 ,即有
,即有
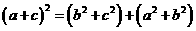 ,
,
注意到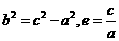 ,变形得
,变形得 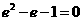 ,从而
,从而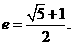
说明:类比推理、类比发现是今年高考的一个新的亮点.这种问题的情景比较清新,结构比较巧妙,变化比较合理,是用"活题"考能力的典范.
例18 (2005年重庆高考试题)连接抛物线上任意四点组成的四边形可能是 (填写所有正确选项的序号).
①菱形 ②有3条边相等的四边形 ③梯形
④平行四边形 ⑤有一组对角相等的四边形
点通:①菱形不可能.如果这个四边形是菱形,那么菱形的一条对角线垂直抛物线的对称轴,这时四边形的必有一个顶点在抛物线的对称轴上(非抛物线的顶点);④平行四边形也不可能.因为抛物上四个点组成的四边形最多有一组对边平行.故连接抛物线上任意四点组成的四边形可能是②③⑤.
说明:针对②③⑤,你能构造出具体的图形吗?
 已知正数
已知正数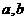 满足
满足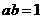 ,则
,则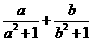 的最大值是_________.
的最大值是_________. 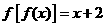 的一个函数是________.
的一个函数是________. 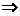 ()t,
()t, 例15 三棱柱
例15 三棱柱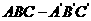 的体积为1,P为侧棱
的体积为1,P为侧棱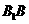 上的一点,则四棱锥
上的一点,则四棱锥 的体积为____________.
的体积为____________. 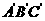 的距离分别为
的距离分别为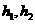 ,则棱柱的高为
,则棱柱的高为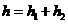 ,又记
,又记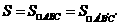 ,则三棱柱的体积为
,则三棱柱的体积为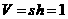 .而从三棱柱中取去四棱锥
.而从三棱柱中取去四棱锥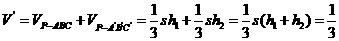 ,
,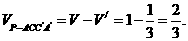
 例16 正三棱锥P-ABC的底面边长为1,E、F、G、H分别是PA、 AC、BC、PB的中点,四边形EFGH的面积为S,则S的取值范围是
.
例16 正三棱锥P-ABC的底面边长为1,E、F、G、H分别是PA、 AC、BC、PB的中点,四边形EFGH的面积为S,则S的取值范围是
.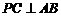 ,因而四边形
,因而四边形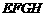 为矩形.设正三棱锥的侧棱
为矩形.设正三棱锥的侧棱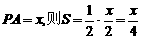 ,设
,设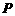 在平面上的射影为
在平面上的射影为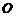 ,连
,连 ,则
,则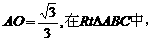
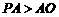 ,从而
,从而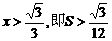 .故应填
.故应填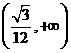 .
.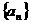 是公差不为零的等差数列,如果
是公差不为零的等差数列,如果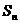 是
是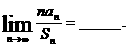
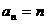 ,有
,有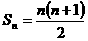 ,于是有
,于是有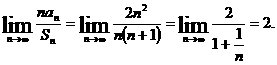 故应填2.
故应填2.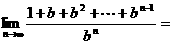 .
.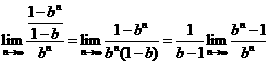 =
=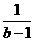 .
.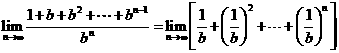
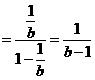 .
.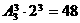 种,再将7、8插入4个空位中的两个有
种,再将7、8插入4个空位中的两个有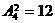 种,故有
种,故有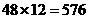 种.
种.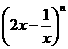 的各项系数的绝对值之和为729,则展开式中的常数项是
.
的各项系数的绝对值之和为729,则展开式中的常数项是
.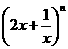 展开式的各项系数之和,取
展开式的各项系数之和,取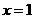 ,得
,得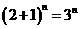 ,则有
,则有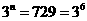 ,所以
,所以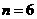 .于是
.于是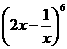 的通项为
的通项为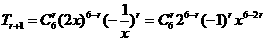 .
.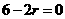 ,得
,得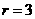 .所以常数项为
.所以常数项为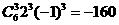 .
.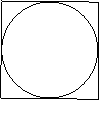 点通:因为正方形的面积是16,内切圆的面积是
点通:因为正方形的面积是16,内切圆的面积是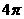 ,所以豆子落入圆内的概率是
,所以豆子落入圆内的概率是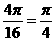 .
.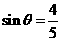 ,且
,且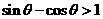 ,则
,则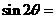 ________.
________.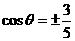 .而有条件
.而有条件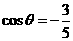 ,
,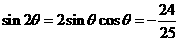 .
.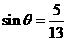 时,
时,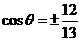 .看看上面的"读出",“取舍”,“用公式”,想想解题思维的流程,会有什么启发?
.看看上面的"读出",“取舍”,“用公式”,想想解题思维的流程,会有什么启发?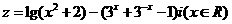 在复平面内对应的点位于第______象限.
在复平面内对应的点位于第______象限.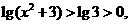 而由
而由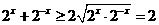 ,知道
,知道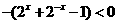 .
.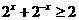 你能直接看出来吗?复数在高考中是一个淡化的知识点,一般命制一道选择题或填空题.
你能直接看出来吗?复数在高考中是一个淡化的知识点,一般命制一道选择题或填空题.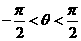 ,且
,且 其中
其中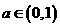 ,则关于
,则关于 的值,在以下四个数值: ①
的值,在以下四个数值: ① 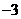 ②
② 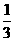 ③
③ 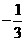 ④
④ 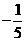
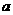 的值可以是________.
的值可以是________.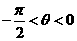 ,从而
,从而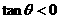 .此时有
.此时有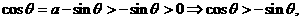
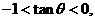 于是,排除①和②,应该填③,④.
于是,排除①和②,应该填③,④.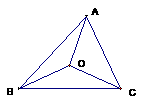 例9 如图,设点O在
例9 如图,设点O在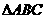 内部,且有
内部,且有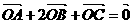 ,则
,则 的面积的比为________.
的面积的比为________.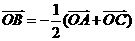 ,所以点O是AC边上的中线的中点,于是,则
,所以点O是AC边上的中线的中点,于是,则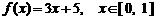 的反函数
的反函数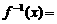 .
.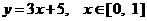 ,得
,得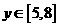 .解出
.解出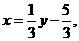 ,从而
,从而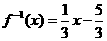 ,
,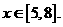 从而应填
从而应填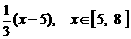 .
.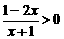 的解集是
.
的解集是
.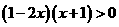 ,也就是
,也就是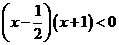 ,所以
,所以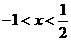 ,从而应填
,从而应填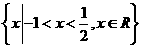 .
.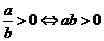 .
.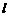 过点
过点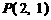 ,且与
,且与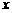 轴、
轴、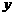 轴的正半轴分别交于
轴的正半轴分别交于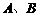 两点,
两点,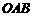 面积的最小值为 .
面积的最小值为 .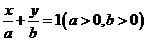 ,则有关系
,则有关系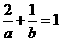 .
.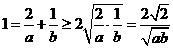 ,即
,即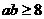 .
.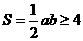 .从而应填4.
.从而应填4.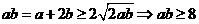 .特别注意,不等式中的等号是可以成立的.
.特别注意,不等式中的等号是可以成立的.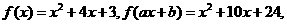 则
则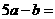 .
.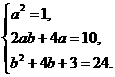
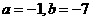 , 或
, 或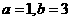 ,所以
,所以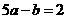 .
.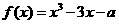 在区间
在区间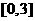 上的最大值和最小值之差为_______.
上的最大值和最小值之差为_______.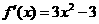 .易知当
.易知当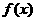 取得最小值
取得最小值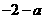 ;当
;当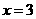 时,函数
时,函数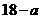 ,后者与前者的差为20.
,后者与前者的差为20.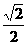 .
14. ①③. 15.
.
14. ①③. 15. 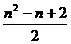 . 16.
. C,3.
. 16.
. C,3.