摘要:质地均匀的正方体木块的棱长为n,n为正整数且n≥2.在其表面涂上与材质颜色不同的蓝色后将木块分割成棱长为1的小正方体木块,假设从中任意取一块得到表面有蓝色的木块的概率为P,请研究P能否大于或小于. [解答]:当n=2时, P=1; 当n≥3时,有P=, P-=. 记y=g(x)= , x>2. g′(x)= , 可知在上y= g(x)只有一个极大值点x=, 所以函数y= g(x)在(2, )上是增函数;在(,+∞)上是减函数. 又验证g(3)>0, g(9) >0, g(10)<0, 于是我们得到结论:当正整数2≤n≤9时, P>;当正整数n≥10时, P<.
网址:http://m.1010jiajiao.com/timu3_id_501423[举报]
先将一个棱长为3的正方体木块的六个面分别涂上六种颜色,再将该正方体均匀切割成棱长为1的小正方体,现从切好的小正方体中任取一块,所得正方体的六个面均没有涂色的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
先将一个棱长为3的正方体木块的六个面分别涂上六种颜色,再将该正方体均匀切割成棱长为1的小正方体,现从切好的小正方体中任取一块,所得的小正方体中六个面均没有涂色的有( )
A.4个 B.3个 C.2个 D.1个
查看习题详情和答案>>先将一个棱长为3的正方体木块的六个面分别涂上颜色,再将该正方体均匀切割成棱长为1的小正方体,现从切好的小正方体中任取一块,则所得正方体的六个面均没有涂色的概率是( )
A. B.
B.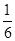
C.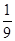 D.
D.
查看习题详情和答案>>