0 50128 50136 50142 50146 50152 50154 50158 50164 50166 50172 50178 50182 50184 50188 50194 50196 50202 50206 50208 50212 50214 50218 50220 50222 50223 50224 50226 50227 50228 50230 50232 50236 50238 50242 50244 50248 50254 50256 50262 50266 50268 50272 50278 50284 50286 50292 50296 50298 50304 50308 50314 50322 447348
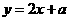 与
与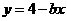 互为反函数,则
互为反函数,则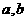 的值分别为( )
的值分别为( )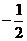 D.
D. 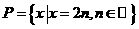 ,
,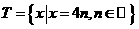 ,则
,则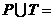 ( )
( )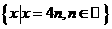 B.
B.
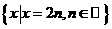
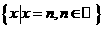 D.
D. 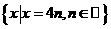
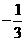 ; 15.
; 15. 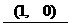 ;
;  .
.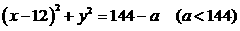 可知圆心M的坐标为(12,0),
依题意:
可知圆心M的坐标为(12,0),
依题意: 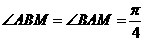 ,
, 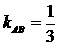 ,
, 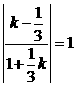 ,解得:
,解得: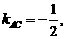
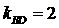 …… (2分)
…… (2分) 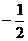 ,
,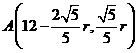 ,
,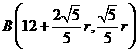 …………(6分)
…………(6分)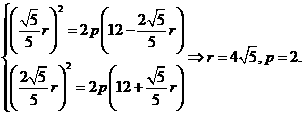
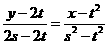
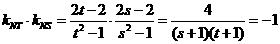
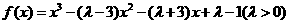 在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.
在区间[n,m]上为减函数,记m的最大值为m0,n的最小值为n 0,且有m0- n 0=4.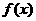 的解析式;
的解析式;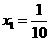 ,公差
,公差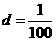 .又过点
.又过点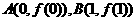 的直线方程为
的直线方程为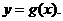 试问:在数列{xn}中,哪些项满足
试问:在数列{xn}中,哪些项满足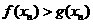 ?
?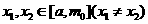 ,都有
,都有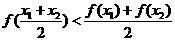 成立,求a的最小值.
成立,求a的最小值.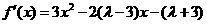 由题意可知
由题意可知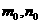 为方程
为方程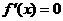 的两根
的两根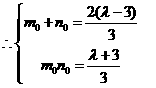 其中
其中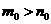
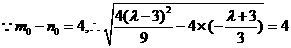
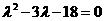 解得
解得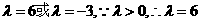
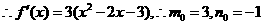
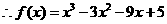
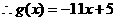 6/
6/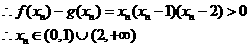
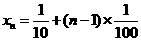 可解得
可解得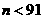 或
或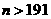
 当
当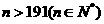 时,满足题意 (3)
时,满足题意 (3)
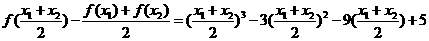
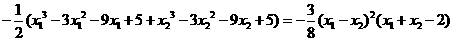 由题意,
由题意,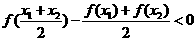 恒成立,即
恒成立,即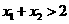 恒成立
恒成立 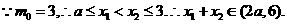
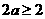 成立,即只要
成立,即只要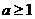 成立
成立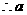 的最小值为1
的最小值为1
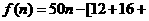 …
…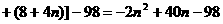 .……… 2分
.……… 2分 ,得
,得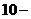
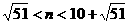 .
.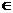 N,故n=3,4,5,…,17 ……………5分
N,故n=3,4,5,…,17 ……………5分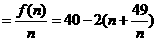 .
.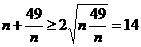 ,当且仅当n=7时取“=”号.…………8分
,当且仅当n=7时取“=”号.…………8分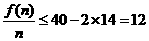 (万元).……………9分
(万元).……………9分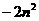 +40n-98=-2
+40n-98=-2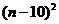 +102.
+102.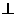 平面EBD;
平面EBD; 又BD
又BD BE=B, ∴A1C⊥平面EBD. …… (4分)
BE=B, ∴A1C⊥平面EBD. …… (4分) 平面A1B1C,AB
平面A1B1C,AB 平面A1B1C,
平面A1B1C, 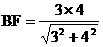
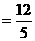 ,
, 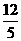 .…… (8分)
.…… (8分)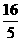 , CF=
, CF=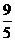 , EF=
, EF=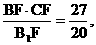 EC=
EC=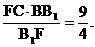
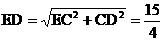 ,……(11分)
,……(11分)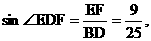 即ED与平面A1B1C所成角为
即ED与平面A1B1C所成角为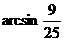 .……(12分)
.……(12分)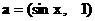 ,
, 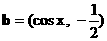 .
.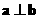 时, 求
时, 求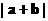 的值; (2) 求函数
的值; (2) 求函数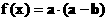 的值域.
的值域.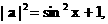
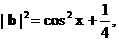
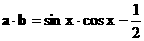 …… (3分)
…… (3分)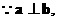 ∴
∴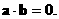 ……(4分) 又
……(4分) 又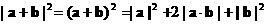
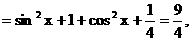 ∴
∴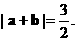 ……(7分)
……(7分)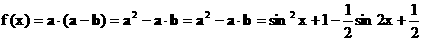 ……(8分)
……(8分)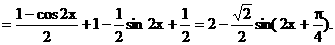 ……(10分)
……(10分)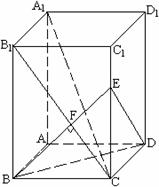 ∴
∴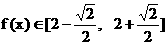 .……(12分)
.……(12分)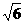 , 则半球的体积为 .
, 则半球的体积为 .