摘要:23. 解:(1)∵⊙P分别与两坐标轴相切. ∴ PA⊥OA.PK⊥OK. ∴∠PAO=∠OKP=90°. 又∵∠AOK=90°. ∴ ∠PAO=∠OKP=∠AOK=90°. ∴四边形OKPA是矩形. 又∵OA=OK. ∴四边形OKPA是正方形.--------2分 (2)①连接PB.设点P的横坐标为x.则其纵坐标为. 过点P作PG⊥BC于G. ∵四边形ABCP为菱形. ∴BC=PA=PB=PC. ∴△PBC为等边三角形. 在Rt△PBG中.∠PBG=60°.PB=PA=x. PG=. sin∠PBG=.即. 解之得:x=±2. ∴ PG=.PA=BC=2.--------4分 易知四边形OGPA是矩形.PA=OG=2.BG=CG=1. ∴OB=OG-BG=1.OC=OG+GC=3. ∴ A(0.).B(1.0) C(3.0).--------6分 设二次函数解析式为:y=ax2+bx+c. 据题意得: 解之得:a=. b=. c=. ∴二次函数关系式为:.--------9分 ②解法一:设直线BP的解析式为:y=ux+v.据题意得: 解之得:u=. v=. ∴直线BP的解析式为:. 过点A作直线AM∥PB.则可得直线AM的解析式为:. 解方程组: 得: , . 过点C作直线CM∥PB.则可设直线CM的解析式为:. ∴0=. ∴. ∴直线CM的解析式为:. 解方程组: 得: , . 综上可知.满足条件的M的坐标有四个. 分别为:(0.).(3.0).(4.).(7.).-------12分 解法二:∵. ∴A(0.).C(3.0)显然满足条件. 延长AP交抛物线于点M.由抛物线与圆的轴对称性可知.PM=PA. 又∵AM∥BC. ∴. ∴点M的纵坐标为. 又点M的横坐标为AM=PA+PM=2+2=4. ∴点M(4.)符合要求. 点(7.)的求法同解法一. 综上可知.满足条件的M的坐标有四个. 分别为:(0.).(3.0).(4.).(7.).-------12分 解法三:延长AP交抛物线于点M.由抛物线与圆的轴对称性可知.PM=PA. 又∵AM∥BC. ∴. ∴点M的纵坐标为. 即. 解得:(舍).. ∴点M的坐标为(4.). 点(7.)的求法同解法一. 综上可知.满足条件的M的坐标有四个. 分别为:(0.).(3.0).(4.).(7.).-------12分
网址:http://m.1010jiajiao.com/timu3_id_493973[举报]
(2012•宜昌)如图,在平面直角坐标系中,直线y=
x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x-m)2+n经过点E.⊙M与x轴、直线AB都相切,其半径为3(1-
)a.
(1)求点A的坐标和∠ABO的度数;
(2)当点C与点A重合时,求a的值;
(3)点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?
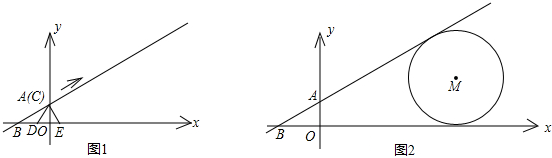
查看习题详情和答案>>
| ||
| 3 |
| 3 |
(1)求点A的坐标和∠ABO的度数;
(2)当点C与点A重合时,求a的值;
(3)点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?
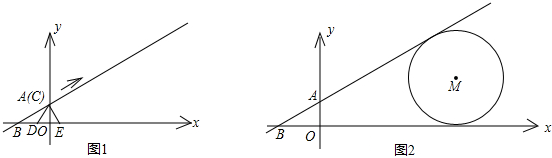
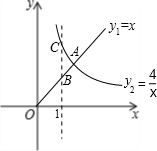 函数y1=x(x≥0),y2=
函数y1=x(x≥0),y2= 10、如图,在平面直角坐标系中,⊙O′与两坐标分别交于A,B,C,D四点,已知:A(6,0),B(0,-3),C(-2,0),则点D的坐标为( )
10、如图,在平面直角坐标系中,⊙O′与两坐标分别交于A,B,C,D四点,已知:A(6,0),B(0,-3),C(-2,0),则点D的坐标为( )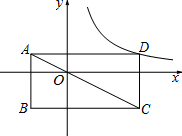 如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D在反比例函数
如图,矩形ABCD的边分别与两坐标轴平行,对角线AC经过坐标原点,点D在反比例函数 如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°.
如图,⊙C经过原点且与两坐标分别交于点A与点B,点A的坐标为(0,6),点M是圆上弧BO的中点,且∠BMO=120°.