2.第(2)问中,①②③任意写对一条得1分;其它结论参照给分.
58(08江西省卷25题)(本大题10分)如图1,正方形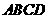 和正三角形
和正三角形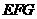 的边长都为1,点
的边长都为1,点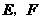 分别在线段
分别在线段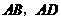 上滑动,设点
上滑动,设点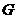 到
到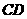 的距离为
的距离为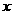 ,到
,到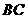 的距离为
的距离为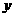 ,记
,记 为
为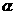 (当点
(当点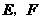 分别与
分别与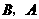 重合时,记
重合时,记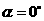 ).
).
(1)当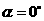 时(如图2所示),求
时(如图2所示),求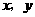 的值(结果保留根号);
的值(结果保留根号);
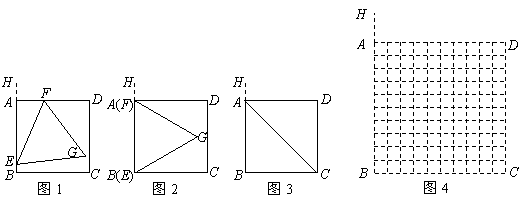
(2)当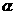 为何值时,点
为何值时,点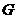 落在对角线
落在对角线 上?请说出你的理由,并求出此时
上?请说出你的理由,并求出此时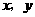 的值(结果保留根号);
的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
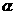 |
 |
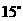 |
 |
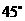 |
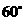 |
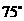 |
 |
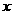 |
|
0.03 |
0 |
|
|
0.29 |
|
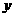 |
|
0.29 |
0.13 |
|
|
0.03 |
|
(4)若将“点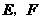 分别在线段
分别在线段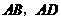 上滑动”改为“点
上滑动”改为“点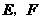 分别在正方形
分别在正方形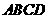 边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点
边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点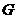 运动所形成的大致图形.
运动所形成的大致图形.
 (参考数据:
(参考数据: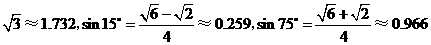 .)
.)
 (08江西省卷25题解析)解:(1)过
(08江西省卷25题解析)解:(1)过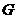 作
作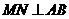 于
于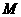 交
交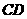 于
于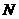 ,
,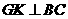 于
于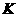 .
.
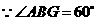 ,
,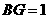 ,
,
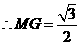 ,
,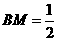 .
.
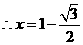 ,
,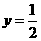 .······························································································· 2分
.······························································································· 2分
(2)当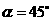 时,点
时,点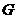 在对角线
在对角线 上,其理由是:················································ 3分
上,其理由是:················································ 3分
过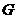 作
作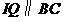 交
交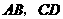 于
于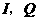 ,
,
 过
过 作
作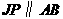 交
交 于
于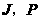 .
.
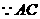 平分
平分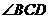 ,
,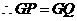 ,
,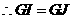 .
.
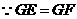 ,
,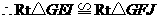 ,
,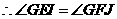 .
.
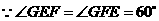 ,
,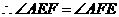 .
.
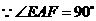 ,
,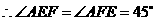 .
.
即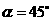 时,点
时,点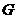 落在对角线
落在对角线 上.······································································ 4分
上.······································································ 4分
(以下给出两种求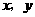 的解法)
的解法)
方法一: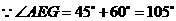 ,
,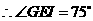 .
.
在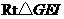 中,
中,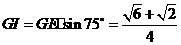 ,
,
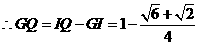 .················································································ 5分
.················································································ 5分
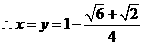 .······························································································ 6分
.······························································································ 6分
方法二:当点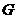 在对角线
在对角线 上时,有
上时,有
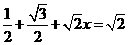 ,································································································· 5分
,································································································· 5分
解得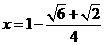
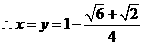 .······························································································ 6分
.······························································································ 6分
(3)
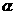 |
 |
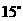 |
 |
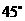 |
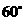 |
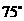 |
 |
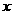 |
0.13 |
0.03 |
0 |
0.03 |
0.13 |
0.29 |
0.50 |
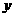 |
0.50 |
0.29 |
0.13 |
0.03 |
0 |
0.03 |
0.13 |
········································································ 8分
(4)由点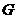 所得到的大致图形如图所示:
所得到的大致图形如图所示:

 ···················································································· 10分
···················································································· 10分
说明:1.第(1)问中,写对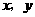 的值各得1分;
的值各得1分;
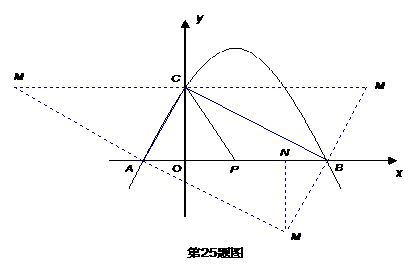
63.(08湖北十堰25题) 已知抛物线
已知抛物线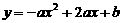 与
与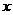 轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
轴的一个交点为A(-1,0),与y轴的正半轴交于点C.
⑴直接写出抛物线的对称轴,及抛物线与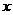 轴的另一个交点B的坐标;
轴的另一个交点B的坐标;
⑵当点C在以AB为直径的⊙P上时,求抛物线的解析式;
⑶坐标平面内是否存在点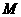 ,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点
,使得以点M和⑵中抛物线上的三点A、B、C为顶点的四边形是平行四边形?若存在,请求出点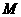 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
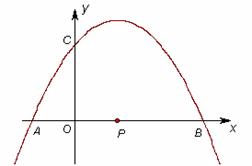
(08湖北十堰25题解析)解:⑴对称轴是直线: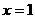 ,点B的坐标是(3,0). ……2分
,点B的坐标是(3,0). ……2分
说明:每写对1个给1分,“直线”两字没写不扣分.
⑵如图,连接PC,∵点A、B的坐标分别是A(-1,0)、B (3,0),
∴AB=4.∴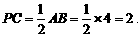
在Rt△POC中,∵OP=PA-OA=2-1=1,
∴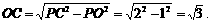
∴b=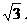 ………………………………3分
………………………………3分
当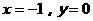 时,
时,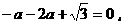
∴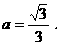 ………………………………4分
………………………………4分
∴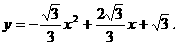 ………………5分
………………5分
⑶存在.……………………………6分
理由:如图,连接AC、BC.设点M的坐标为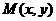 .
.
①当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB.
由⑵知,AB=4,∴|x|=4,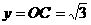 .
.
∴x=±4.∴点M的坐标为 .…9分
.…9分
说明:少求一个点的坐标扣1分.
②当以AB为对角线时,点M在x轴下方.
过M作MN⊥AB于N,则∠MNB=∠AOC=90°.
∵四边形AMBC是平行四边形,∴AC=MB,且AC∥MB.
∴∠CAO=∠MBN.∴△AOC≌△BNM.∴BN=AO=1,MN=CO=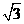 .
.
∵OB=3,∴0N=3-1=2.
∴点M的坐标为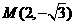 .
……………………………12分
.
……………………………12分
说明:求点M的坐标时,用解直角三角形的方法或用先求直线解析式,
然后求交点M的坐标的方法均可,请参照给分.
综上所述,坐标平面内存在点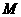 ,使得以点A、B、C、M为顶点的四边形是平行四边形.其坐标为
,使得以点A、B、C、M为顶点的四边形是平行四边形.其坐标为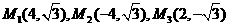 .
.
说明:①综上所述不写不扣分;②如果开头“存在”二字没写,但最后解答全部正确,不扣分。
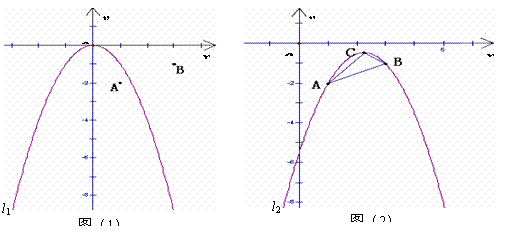
64(08湖南株洲23题)如图(1),在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,-1),二次函数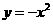 的图象为
的图象为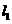 .
.
(1)平移抛物线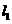 ,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可).
,使平移后的抛物线过点A,但不过点B,写出平移后的抛物线的一个解析式(任写一个即可).
(2)平移抛物线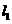 ,使平移后的抛物线过A、B两点,记抛物线为
,使平移后的抛物线过A、B两点,记抛物线为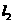 ,如图(2),求抛物线
,如图(2),求抛物线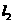 的函数解析式及顶点C的坐标.
的函数解析式及顶点C的坐标.
(3)设P为y轴上一点,且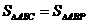 ,求点P的坐标.
,求点P的坐标.
(4)请在图(2)上用尺规作图的方式探究抛物线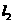 上是否存在点Q,使
上是否存在点Q,使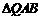 为等腰三角形. 若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
为等腰三角形. 若存在,请判断点Q共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.
(08湖南株洲23题解析)
(1) 等 (满足条件即可) ……1分
等 (满足条件即可) ……1分
(2)设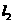 的解析式为
的解析式为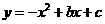 ,联立方程组
,联立方程组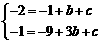 ,
,
解得: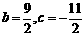 ,则
,则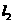 的解析式为
的解析式为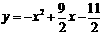 ,
……3分
,
……3分
点C的坐标为(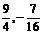 )
……4分
)
……4分
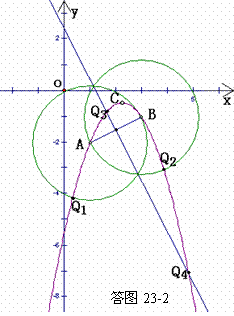
(3)如答图23-1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,则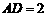 ,
,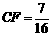 ,
,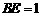 ,
,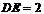 ,
,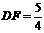 ,
,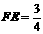 .
.
得: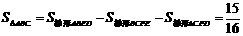 .
……5分
.
……5分
延长BA交y轴于点G,直线AB的解析式为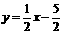 ,则点G的坐标为(0,
,则点G的坐标为(0,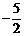 ),设点P的坐标为(0,
),设点P的坐标为(0,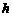 )
)
①当点P位于点G的下方时,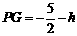 ,连结AP、BP,则
,连结AP、BP,则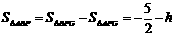 ,又
,又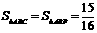 ,得
,得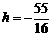 ,点P的坐标为(0,
,点P的坐标为(0,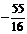 ).
…… 6分
).
…… 6分
②当点P位于点G的上方时,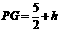 ,同理
,同理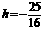 ,点P的坐标为(0,
,点P的坐标为(0,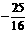 ).
).
综上所述所求点P的坐标为(0,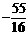 )或(0,
)或(0,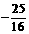 ) ……
7分
) ……
7分
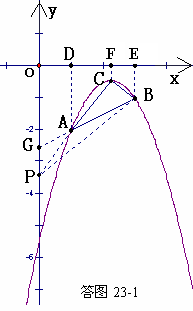
(4) 作图痕迹如答图23-2所示.
由图可知,满足条件的点有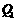 、
、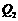 、
、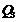 、
、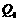 ,共4个可能的位置. …… 10分
,共4个可能的位置. …… 10分
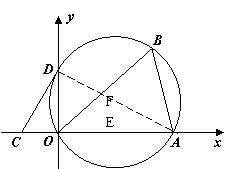
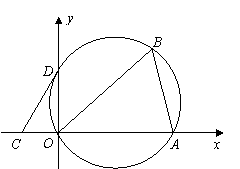
65(08四川达州23题)如图,将 置于平面直角坐标系中,其中点
置于平面直角坐标系中,其中点 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为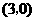 ,
,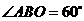 .
.
(1)若 的外接圆与
的外接圆与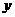 轴交于点
轴交于点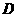 ,求
,求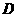 点坐标.
点坐标.
(2)若点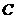 的坐标为
的坐标为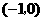 ,试猜想过
,试猜想过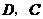 的直线与
的直线与 的外接圆的位置关系,并加以说明.
的外接圆的位置关系,并加以说明.
(3)二次函数的图象经过点 和
和 且顶点在圆上,
且顶点在圆上,
求此函数的解析式.
(08四川达州23题解析)解:(1)连结AD,则∠ADO=∠B=600
在Rt△ADO中,∠ADO=600
所以OD=OA÷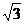 =3÷
=3÷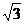 =
=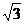
|
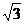 )
)
(2)猜想是CD与圆相切
∵ ∠AOD是直角,所以AD是圆的直径
|
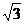 =
=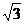 , ∠CDO=300
, ∠CDO=300
∴∠CDA=∠CDO+∠ADO=Rt∠ 即CD⊥AD
∴ CD切外接圆于点D
(3)依题意可设二次函数的解析式为 :
y=α(x-0)(x-3)
由此得顶点坐标的横坐标为:x=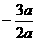 =
=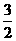 ;
;
即顶点在OA的垂直平分线上,作OA的垂直平分线EF,则得∠EFA=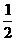 ∠B=300
∠B=300
得到EF=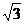 EA=
EA=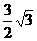 可得一个顶点坐标为(
可得一个顶点坐标为(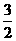 ,
,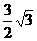 )
)
同理可得另一个顶点坐标为(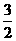 ,
,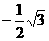 )
)
分别将两顶点代入y=α(x-0)(x-3)可解得α的值分别为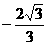 ,
,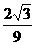
则得到二次函数的解析式是y=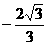 x(x-3)或y=
x(x-3)或y=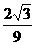 x(x-3)
x(x-3)
 66(08安徽芜湖24题)如图,已知
66(08安徽芜湖24题)如图,已知 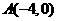 ,
,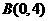 ,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
(1) 求C点坐标及直线BC的解析式;
(2) 一抛物线经过B、C两点,且顶点落在x轴正半轴上,求该抛物线的解析式并画出函数图象;
(3)
现将直线BC绕B点旋转与抛物线相交与另一点P,请找出抛物线上所有满足到直线AB距离为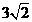 的点P.
的点P.
解:
(08安徽芜湖24题解析)解: (1)
过C点向x轴作垂线,垂足为D,由位似图形性质可知:
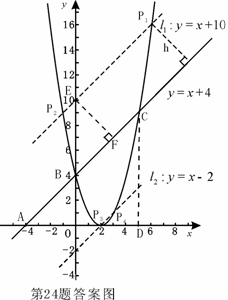 △ABO∽△ACD, ∴
△ABO∽△ACD, ∴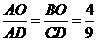 .
.
由已知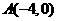 ,
,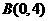 可知:
可知: 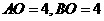 .
.
∴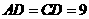 .∴C点坐标为
.∴C点坐标为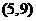 .·················· 2分
.·················· 2分
直线BC的解析是为: 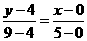
化简得: 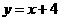 ·················································· 3分
·················································· 3分
(2)设抛物线解析式为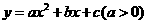 ,由题意得:
,由题意得: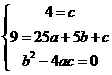 ,
,
解得: 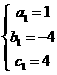 ,
,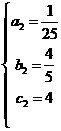
∴解得抛物线解析式为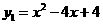 或
或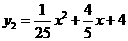 .
.
又∵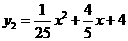 的顶点在x轴负半轴上,不合题意,故舍去.
的顶点在x轴负半轴上,不合题意,故舍去.
∴满足条件的抛物线解析式为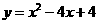 ······························································· 5分
······························································· 5分
(准确画出函数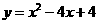 图象)········································································· 7分
图象)········································································· 7分
(3) 将直线BC绕B点旋转与抛物线相交与另一点P,设P到 直线AB的距离为h,
故P点应在与直线AB平行,且相距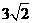 的上下两条平行直线
的上下两条平行直线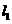 和
和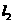 上.······················ 8分
上.······················ 8分
由平行线的性质可得:两条平行直线与y轴的交点到直线BC的距离也为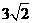 .
.
如图,设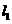 与y轴交于E点,过E作EF⊥BC于F点,
与y轴交于E点,过E作EF⊥BC于F点,
在Rt△BEF中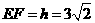 ,
,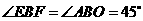 ,
,
∴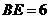 .∴可以求得直线
.∴可以求得直线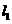 与y轴交点坐标为
与y轴交点坐标为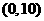 ·············································· 10分
·············································· 10分
同理可求得直线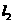 与y轴交点坐标为
与y轴交点坐标为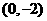 ································································· 11分
································································· 11分
∴两直线解析式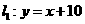 ;
;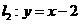 .
.
根据题意列出方程组: ⑴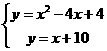 ;⑵
;⑵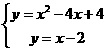
∴解得: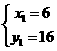 ;
;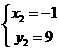 ;
;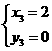 ;
;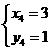
∴满足条件的点P有四个,它们分别是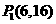 ,
,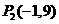 ,
,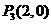 ,
,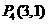 ········ 15分
········ 15分
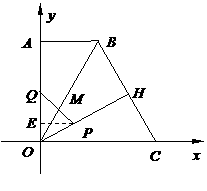
67(08湖北仙桃等4市25题)如图,直角梯形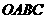 中,
中,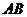 ∥
∥ ,
, 为坐标原点,点
为坐标原点,点 在
在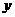 轴正半轴上,点
轴正半轴上,点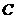 在
在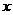 轴正半轴上,点
轴正半轴上,点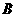 坐标为(2,2
坐标为(2,2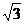 ),∠
),∠ = 60°,
= 60°,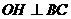 于点
于点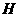 .动点
.动点 从点
从点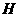 出发,沿线段
出发,沿线段 向点
向点 运动,动点
运动,动点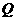 从点
从点 出发,沿线段
出发,沿线段 向点
向点 运动,两点同时出发,速度都为每秒1个单位长度.设点
运动,两点同时出发,速度都为每秒1个单位长度.设点 运动的时间为
运动的时间为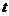 秒.
秒.
(1)
求 的长;
的长;
(2)
若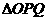 的面积为
的面积为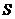 (平方单位). 求
(平方单位). 求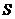 与
与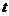 之间的函数关系式.并求
之间的函数关系式.并求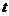 为何值时,
为何值时,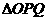 的面积最大,最大值是多少?
的面积最大,最大值是多少?
(3)
设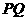 与
与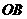 交于点
交于点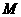 .①当△
.①当△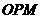 为等腰三角形时,求(2)中
为等腰三角形时,求(2)中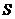 的值.
的值.
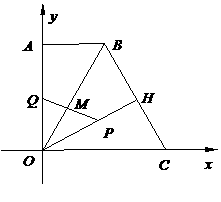 ②探究线段
②探究线段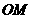 长度的最大值是多少,直接写出结论.
长度的最大值是多少,直接写出结论.
(08湖北仙桃等4市25题解析)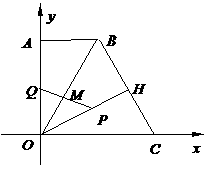 解:(1)∵
解:(1)∵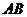 ∥
∥
∴ 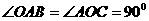
在 中,
中,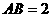 ,
,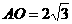
∴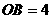 ,
, 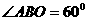
∴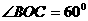 而
而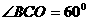
∴ 为等边三角形
为等边三角形
∴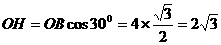 …(3分)
…(3分)
(2)∵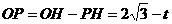
∴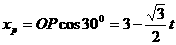
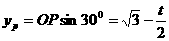
∴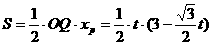
=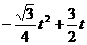 (
(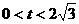 )…………………………(6分)
)…………………………(6分)
即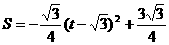
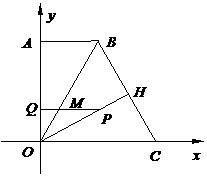 ∴当
∴当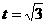 时,
时,
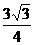 ………………………………………(7分)
………………………………………(7分)
(3)①若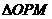 为等腰三角形,则:
为等腰三角形,则:
(i)若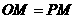 ,
,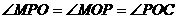
∴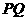 ∥
∥
∴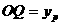 即
即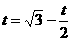
解得: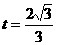
 此时
此时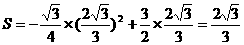 ………………………………(8分)
………………………………(8分)
(ii)若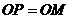 ,
,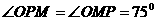
∴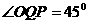
过 点作
点作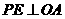 ,垂足为
,垂足为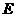 ,则有:
,则有:
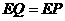
即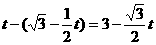
解得: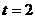
此时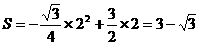 ……………………………………(9分)
……………………………………(9分)
(iii)若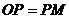 ,
,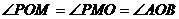
∴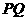 ∥
∥
此时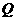 在
在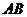 上,不满足题意.……………………………………………(10分)
上,不满足题意.……………………………………………(10分)
②线段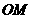 长的最大值为
长的最大值为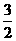 ……………………………………………………(12分)
……………………………………………………(12分)
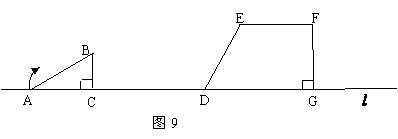
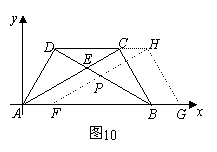
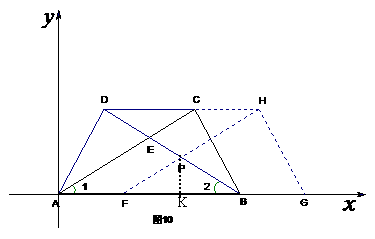
68(08湖南常德26题)如图9,在直线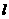 上摆放有△ABC和直角梯形DEFG,且CD=6㎝;在△ABC中:∠C=90O,∠A=300,AB=4㎝;在直角梯形DEFG中:EF//DG,∠DGF=90O ,DG=6㎝,DE=4㎝,∠EDG=600。解答下列问题:
上摆放有△ABC和直角梯形DEFG,且CD=6㎝;在△ABC中:∠C=90O,∠A=300,AB=4㎝;在直角梯形DEFG中:EF//DG,∠DGF=90O ,DG=6㎝,DE=4㎝,∠EDG=600。解答下列问题:
(1)旋转:将△ABC绕点C顺时针方向旋转900,请你在图中作出旋转后的对应图形
△A1B1C,并求出AB1的长度;
(2)翻折:将△A1B1C沿过点B1且与直线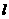 垂直的直线翻折,得到翻折后的对应图形
垂直的直线翻折,得到翻折后的对应图形
△A2B1C1,试判定四边形A2B1DE的形状?并说明理由;
(3)平移:将△A2B1C1沿直线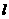 向右平移至△A3B2C2,若设平移的距离为x,△A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC面积的一半时,x的值是多少?
向右平移至△A3B2C2,若设平移的距离为x,△A3B2C2与直角梯形重叠部分的面积为y,当y等于△ABC面积的一半时,x的值是多少?
(08湖南常德26题解析)
解:(1)在△ABC中由已知得:BC=2,AC=AB×cos30°=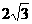 ,
,
∴AB1=AC+C B1=AC+CB=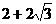 .……………………………………2分
.……………………………………2分
(2)四边形A2B1DE为平行四边形.理由如下:
∵∠EDG=60°,∠A2B1C1=∠A1B1C=∠ABC=60°,∴A2B1∥DE
又A2B1=A1B1=AB=4,DE=4,∴A2B1=DE,故结论成立.………………4分
(3)由题意可知:
S△ABC=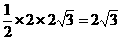 ,
,
①
当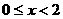 或
或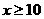 时,y=0
时,y=0
此时重叠部分的面积不会等于△ABC的面积的一半……………5分
②当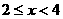 时,直角边B2C2与等腰梯形的下底边DG重叠的长度为DC2=C1C2-DC1=(x-2)㎝,则y=
时,直角边B2C2与等腰梯形的下底边DG重叠的长度为DC2=C1C2-DC1=(x-2)㎝,则y=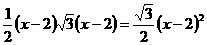 ,
,
当y= 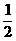 S△ABC=
S△ABC= 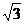 时,即
时,即 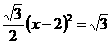 ,
,
解得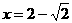 (舍)或
(舍)或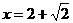 .
.
∴当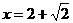 时,重叠部分的面积等于△ABC的面积的一半.
时,重叠部分的面积等于△ABC的面积的一半.
③当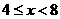 时,△A3B2C2完全与等腰梯形重叠,即
时,△A3B2C2完全与等腰梯形重叠,即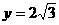 ……………7分
……………7分
④当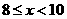 时,B2G=B2C2-GC2=2-(
时,B2G=B2C2-GC2=2-(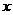 -8)=10-
-8)=10-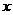
则y=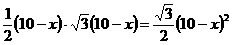 ,
,
当y= 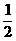 S△ABC=
S△ABC= 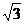 时,即
时,即 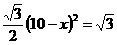 ,
,
解得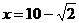 ,或
,或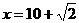 (舍去).
(舍去).
∴当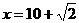 时,重叠部分的面积等于△ABC的面积的一半.………9分
时,重叠部分的面积等于△ABC的面积的一半.………9分
由以上讨论知,当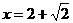 或
或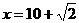 时, 重叠部分的面积等于△ABC的面积的一半.………10分
时, 重叠部分的面积等于△ABC的面积的一半.………10分
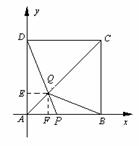
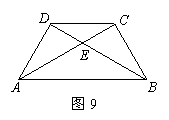
69(08宁夏区卷26题)如图,在边长为4的正方形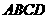 中,点
中,点 在
在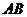 上从
上从 向
向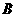 运动,连接
运动,连接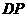 交
交 于点
于点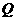 .
.
(1)试证明:无论点 运动到
运动到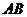 上何处时,都有△
上何处时,都有△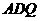 ≌△
≌△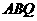 ;
;
(2)当点 在
在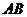 上运动到什么位置时,△
上运动到什么位置时,△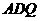 的面积是正方形
的面积是正方形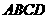 面积的
面积的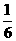 ;
;
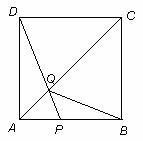 (3)若点
(3)若点 从点
从点 运动到点
运动到点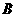 ,再继续在
,再继续在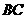 上运动到点
上运动到点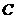 ,在整个运动过程中,当点
,在整个运动过程中,当点 运动到什么位置时,△
运动到什么位置时,△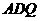 恰为等腰三角形.
恰为等腰三角形.
(08宁夏区卷26题解析)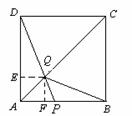 (1)证明:在正方形
(1)证明:在正方形 中,
中,
无论点 运动到
运动到 上何处时,都有
上何处时,都有
 =
=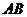 ∠
∠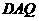 =∠
=∠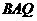
 =
=
∴△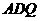 ≌△
≌△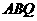 ·············································· 2分
·············································· 2分
(2)解法一:△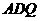 的面积恰好是正方形ABCD面积的
的面积恰好是正方形ABCD面积的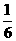 时,
时,
过点Q作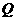
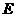 ⊥
⊥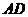 于
于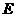 ,
,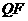 ⊥
⊥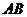 于
于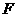 ,则
,则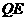 =
= 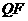
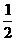
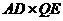 =
=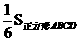 =
=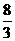
∴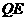 =
=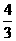 ·········································································································· 4分
·········································································································· 4分
由△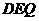 ∽△
∽△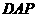 得
得 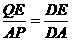 解得
解得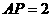
∴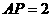 时,△
时,△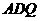 的面积是正方形
的面积是正方形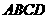 面积的
面积的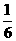 ······························· 6分
······························· 6分
解法二:以 为原点建立如图所示的直角坐标系,过点
为原点建立如图所示的直角坐标系,过点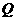 作
作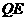 ⊥
⊥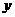 轴于点
轴于点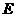 ,
,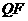 ⊥
⊥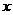 轴于点
轴于点 .
.
 =
=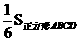 =
=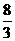 ∴
∴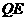 =
=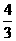
∵点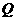 在正方形对角线
在正方形对角线 上 ∴
上 ∴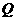 点的坐标为
点的坐标为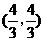
∴ 过点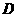 (0,4),
(0,4),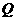 (
(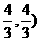 两点的函数关系式为:
两点的函数关系式为: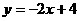
当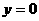 时,
时,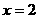 ∴
∴ 点的坐标为(2,0)
点的坐标为(2,0)
∴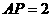 时,△
时,△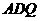 的面积是正方形
的面积是正方形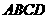 面积的
面积的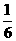 . ······························· 6分
. ······························· 6分
(3)若△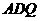 是等腰三角形,则有
是等腰三角形,则有 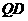 =
=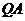 或
或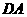 =
=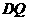 或
或 =
=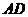
①当点 运动到与点
运动到与点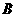 重合时,由四边形
重合时,由四边形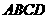 是正方形知
是正方形知 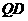 =
=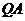
此时△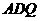 是等腰三角形
是等腰三角形
②当点 与点
与点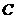 重合时,点
重合时,点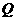 与点
与点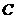 也重合,
也重合,
此时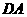 =
=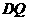 , △
, △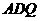 是等腰三角形
································· 8分
是等腰三角形
································· 8分
③解法一:如图,设点 在
在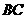 边上运动到
边上运动到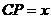 时,有
时,有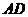 =
=
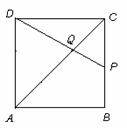 ∵
∵ 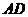 ∥
∥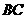 ∴∠
∴∠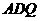 =∠
=∠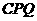
又∵∠ =∠
=∠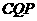 ∠
∠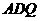 =∠
=∠
∴∠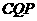 =∠
=∠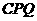
∴  =
=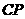 =
=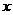
∵ =
=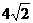
 =
= 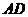 =4
=4
∴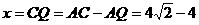
即当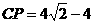 时,△
时,△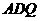 是等腰三角形 ····································· 10分
是等腰三角形 ····································· 10分
解法二:以 为原点建立如图所示的直角坐标系,设点
为原点建立如图所示的直角坐标系,设点 在
在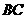 上运动到
上运动到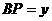 时,有
时,有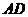 =
= .
.
过点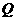 作
作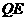 ⊥
⊥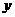 轴于点
轴于点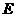 ,
,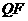 ⊥
⊥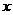 轴于点
轴于点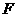 ,则
,则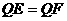
在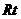 △
△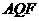 中,
中,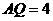 ,∠
,∠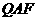 =45°
=45°
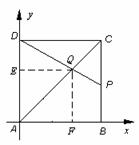 ∴
∴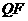 =
=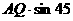 °=
°=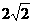
∴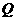 点的坐标为(
点的坐标为(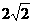 ,
,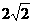 )
)
∴过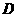 、
、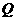 两点的函数关系式:
两点的函数关系式: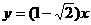 +4
+4
当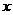 =4时,
=4时,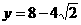 ∴
∴ 点的坐标为(4,8-4
点的坐标为(4,8-4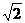 ).
).
∴当点 在
在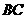 上运动到
上运动到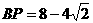 时,△
时,△中,
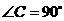 ,
,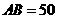 ,
,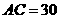 ,
,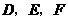 分别是
分别是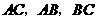 的中点.点
的中点.点 从点
从点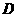 出发沿折线
出发沿折线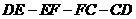 以每秒7个单位长的速度匀速运动;点
以每秒7个单位长的速度匀速运动;点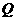 从点
从点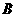 出发沿
出发沿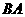 方向以每秒4个单位长的速度匀速运动,过点
方向以每秒4个单位长的速度匀速运动,过点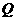 作射线
作射线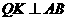 ,交折线
,交折线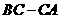 于点
于点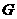 .点
.点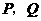 同时出发,当点
同时出发,当点 绕行一周回到点
绕行一周回到点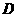 时停止运动,点
时停止运动,点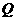 也随之停止.设点
也随之停止.设点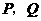 运动的时间是
运动的时间是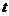 秒(
秒(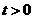 ).
).
(1)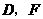 两点间的距离是
;
两点间的距离是
;
(2)射线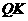 能否把四边形
能否把四边形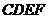 分成面积相等的两部分?若能,求出
分成面积相等的两部分?若能,求出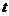 的值.若不能,说明理由;
的值.若不能,说明理由;
(3)当点 运动到折线
运动到折线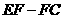 上,且点
上,且点 又恰好落在射线
又恰好落在射线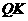 上时,求
上时,求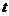 的值;
的值;
 (4)连结
(4)连结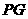 ,当
,当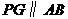 时,请直接写出
时,请直接写出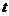 的值.
的值.
(08河北省卷26题解析)解:(1)25.
(2)能.
如图5,连结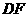 ,过点
,过点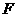 作
作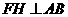 于点
于点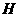 ,
,
由四边形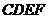 为矩形,可知
为矩形,可知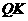 过
过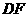 的中点
的中点 时,
时,
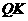 把矩形
把矩形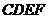 分为面积相等的两部分
分为面积相等的两部分
(注:可利用全等三角形借助割补法或用中心对称等方法说明),
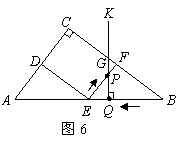
此时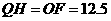 .由
.由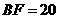 ,
, ,得
,得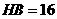 .
.
 故
故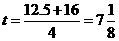 .
.
(3)①当点 在
在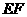 上
上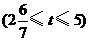 时,如图6.
时,如图6.
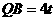 ,
,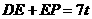 ,
,
 由
由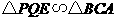 ,得
,得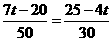 .
.
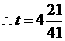 .
.
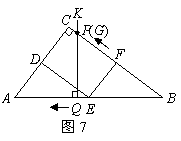
②当点 在
在 上
上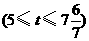 时,如图7.
时,如图7.
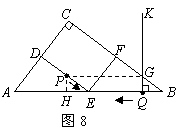 已知
已知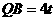 ,从而
,从而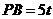 ,
,
由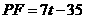 ,
,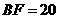 ,得
,得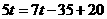 .
.
解得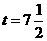 .
.
(4)如图8,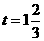 ;如图9,
;如图9,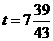 .
.
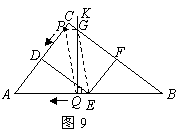
(注:判断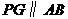 可分为以下几种情形:当
可分为以下几种情形:当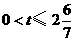 时,点
时,点 下行,点
下行,点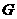 上行,可知其中存在
上行,可知其中存在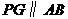 的时刻,如图8;此后,点
的时刻,如图8;此后,点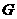 继续上行到点
继续上行到点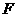 时,
时,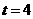 ,而点
,而点 却在下行到点
却在下行到点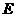 再沿
再沿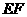 上行,发现点
上行,发现点 在
在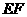 上运动时不存在
上运动时不存在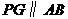 ;当
;当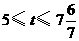 时,点
时,点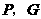 均在
均在 上,也不存在
上,也不存在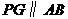 ;由于点
;由于点 比点
比点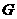 先到达点
先到达点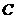 并继续沿
并继续沿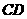 下行,所以在
下行,所以在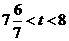 中存在
中存在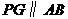 的时刻,如图9;当
的时刻,如图9;当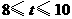 时,点
时,点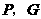 均在
均在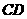 上,不存在
上,不存在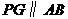 )
)
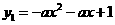 ,
,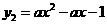 (其中
(其中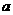 为常数,且
为常数,且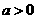 ).
).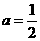 时,设
时,设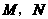 两点(
两点(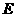 在
在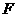 的左边),观察
的左边),观察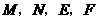 四点坐标,请写出一个你所得到的正确结论,并说明理由;
四点坐标,请写出一个你所得到的正确结论,并说明理由;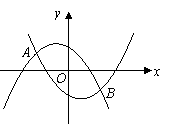 (3)设上述两条抛物线相交于
(3)设上述两条抛物线相交于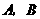 两点,直线
两点,直线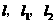 都垂直于
都垂直于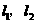 分别经过
分别经过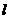 在直线
在直线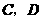 两点,求线段
两点,求线段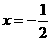 ,或抛物线
,或抛物线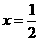 ;
;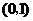 ,或抛物线
,或抛物线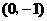 ;
;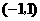 或抛物线
或抛物线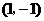 ;
;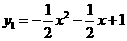 ,令
,令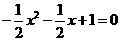 ,
,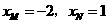 .································································································ 4分
.································································································ 4分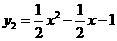 ,令
,令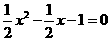 ,解得
,解得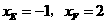 .···························· 5分
.···························· 5分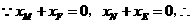 点
点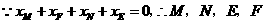 四点横坐标的代数和为0;
四点横坐标的代数和为0;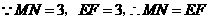 (或
(或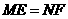 ).················································ 6分
).················································ 6分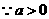 ,
, 抛物线
抛物线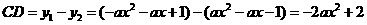 .················· 8分
.················· 8分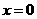 时,
时,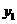 与当
与当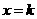 时,
时,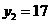 ;且二次函数
;且二次函数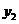 的图象的对称轴是直
的图象的对称轴是直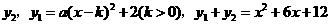 线
线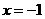 .
.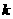 的值;
的值;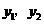 的表达式;
的表达式;
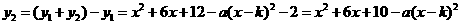 .
. 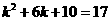 ,
, 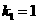 ,或
,或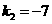 (舍去),故
(舍去),故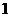 .
. 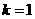 ,得
,得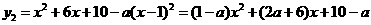 ,
, 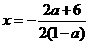 ,
, 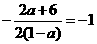 ,解得
,解得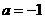 ,
, 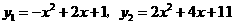 .
. 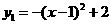 ,得函数
,得函数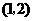 ;
;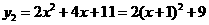 ,得函数
,得函数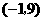 ;
; 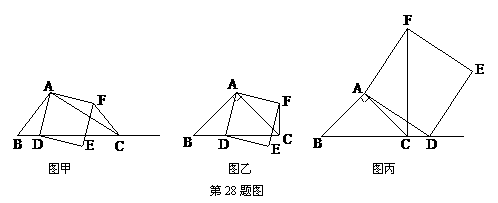 ②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么? ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.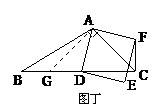 (2)画图正确
(2)画图正确  过点A作AQ⊥BC交BC的延长线于点Q,(如图戊)
过点A作AQ⊥BC交BC的延长线于点Q,(如图戊)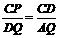 , ∴
, ∴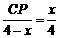 ,
,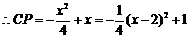 .
. 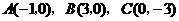 分别代入
分别代入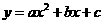 1分
1分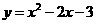 ······································································ 4分
······································································ 4分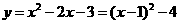 ··············································································· 5分
··············································································· 5分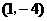 ,对称轴
,对称轴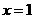 ················································································· 7分
················································································· 7分 ,当
,当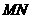 在
在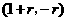 ····························· 8分
····························· 8分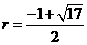 ································································· 9分
································································· 9分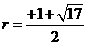
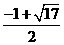 或
或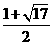 10分
10分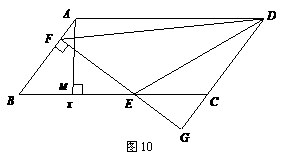
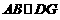 1分
1分
 ···························································································· 3分
···························································································· 3分 的周长之和为定值.····························································· 4分
的周长之和为定值.····························································· 4分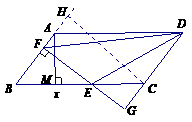 由AB=5,AM=4,可知
由AB=5,AM=4,可知 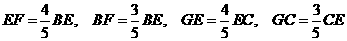 ,
,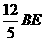 , △ECG的周长是
, △ECG的周长是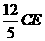
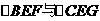 的周长之和是24.·········································· 6分
的周长之和是24.·········································· 6分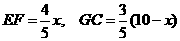
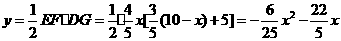 ···································· 8分
···································· 8分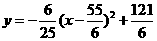 .
. 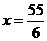 时,y有最大值.············································································· 9分
时,y有最大值.············································································· 9分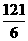 .··········································································································· 10分
.··········································································································· 10分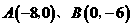 两点.
两点.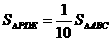 ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.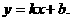
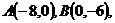 ∴
∴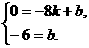 ∴
∴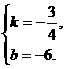
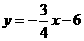 .··································································· 3分
.··································································· 3分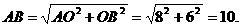
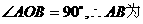 ⊙M的直径,∴半径MA=5,∴N为AO的中点AN=NO=4,∴MN=3∴CN=MC-MN=5-3=2,∴C点的坐标为(-4,2).
⊙M的直径,∴半径MA=5,∴N为AO的中点AN=NO=4,∴MN=3∴CN=MC-MN=5-3=2,∴C点的坐标为(-4,2).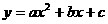
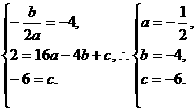
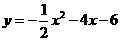 ············································································· 7分
············································································· 7分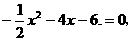 得D、E两点的坐标为D(-6,0)、E(-2,0),所以DE=4.
得D、E两点的坐标为D(-6,0)、E(-2,0),所以DE=4.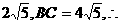 直角三角形的面积
直角三角形的面积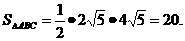
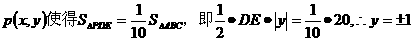 .
.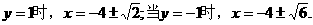 故满足条件的存在.它们是
故满足条件的存在.它们是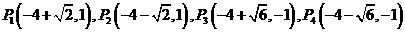 . ························· 10分
. ························· 10分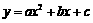 经过点A(5,0)、B(6,-6)和原点.
经过点A(5,0)、B(6,-6)和原点. 与抛物线相交于点C(2,m),请求出
与抛物线相交于点C(2,m),请求出 OBC的面积S的值.
OBC的面积S的值.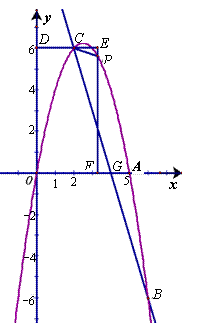 (3)过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴交x轴于点F,交直线DC于点E. 直线PF与直线DC及两坐标轴围成矩形OFED(如图),是否存在点P,使得
(3)过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴交x轴于点F,交直线DC于点E. 直线PF与直线DC及两坐标轴围成矩形OFED(如图),是否存在点P,使得 2分
2分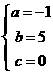 ·················································· 3分
·················································· 3分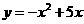 ·············· 4分
·············· 4分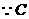 在抛物线上,
在抛物线上,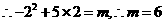 ·· 5分
·· 5分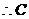 点坐标为(2,6),
点坐标为(2,6),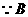 、C在直线
、C在直线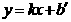 上
上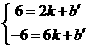 解得
解得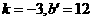
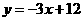 ······································································· 6分
······································································· 6分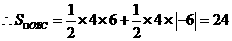 ·································································· 7分
·································································· 7分 ∽
∽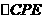 ·············································································· 8分
·············································································· 8分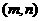 ,
,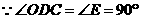
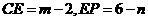
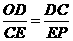 或
或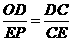
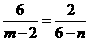 或
或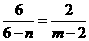
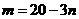 或
或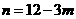
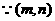 在抛物线上,
在抛物线上,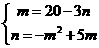 或
或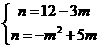
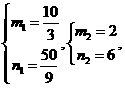 或
或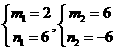
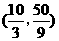 和
和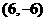 ········································································· 10分
········································································· 10分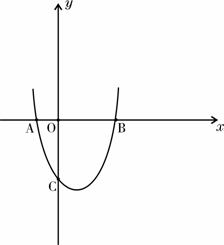
 ,
,
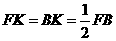 .
.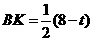 .
.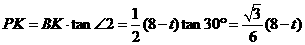 . ……………………7分
. ……………………7分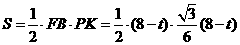 ,
,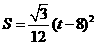 ,或
,或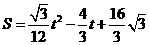 . …………………………………8分
. …………………………………8分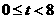 .
…………………………………………………………9分
.
…………………………………………………………9分