0 47920 47928 47934 47938 47944 47946 47950 47956 47958 47964 47970 47974 47976 47980 47986 47988 47994 47998 48000 48004 48006 48010 48012 48014 48015 48016 48018 48019 48020 48022 48024 48028 48030 48034 48036 48040 48046 48048 48054 48058 48060 48064 48070 48076 48078 48084 48088 48090 48096 48100 48106 48114 447348
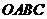 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片, 为原点,点
为原点,点 在
在 轴的正半轴上,点
轴的正半轴上,点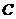 在
在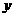 轴的正半轴上,
轴的正半轴上,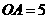 ,
,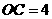 .
. 边上取一点
边上取一点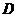 ,将纸片沿
,将纸片沿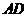 翻折,使点
翻折,使点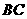 边上的点
边上的点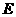 处,求
处,求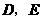 两点的坐标;
两点的坐标;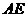 上有一动点
上有一动点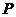 (不与
(不与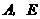 重合)自
重合)自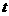 秒(
秒(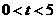 ),过
),过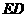 的平行线交
的平行线交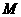 ,过点
,过点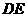 于点
于点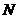 .求四边形
.求四边形 的面积
的面积 与时间
与时间 (3)在(2)的条件下,当
(3)在(2)的条件下,当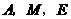 为顶点的三角形为等腰三角形,并求出相应的时刻点
为顶点的三角形为等腰三角形,并求出相应的时刻点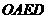 的对称轴,
的对称轴, 在
在 中,
中,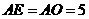 ,
,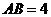 .
.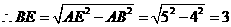 .
.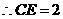 .
.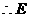 点坐标为(2,4).
点坐标为(2,4).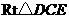 中,
中,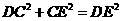 , 又
, 又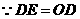 .
.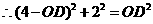 . 解得:
. 解得: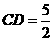 .
.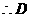 点坐标为
点坐标为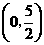
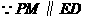 ,
,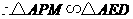 .
.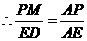 ,又知
,又知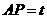 ,
,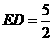 ,
,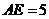
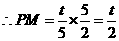 , 又
, 又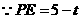 .
.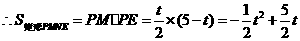
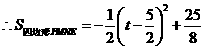 ,又
,又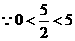
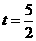 时,
时, 有最大值
有最大值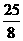 .
.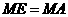 (如图①)
(如图①)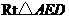 中,
中,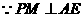 ,
,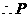 为
为
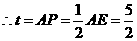 .
.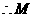 为
为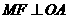 ,垂足为
,垂足为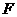 ,则
,则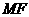 是
是 的中位线,
的中位线,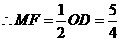 ,
,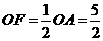 ,
,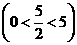 ,
,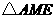 为等腰三角形.
为等腰三角形.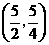 .
.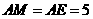 (如图②)
(如图②)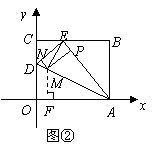 在
在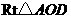 中,
中,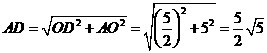 .
.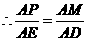 .
.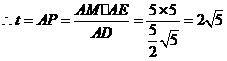 ,
,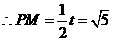 .
.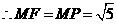 ,
,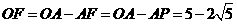 ,
,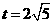 时,(
时,(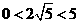 ),此时
),此时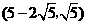 .
.

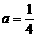 .
.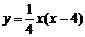 ,即
,即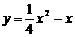 .
.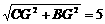 .
. ∴ CB=CE=5.
∴ CB=CE=5. 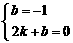 . 解得
. 解得 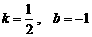 .
.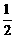 x-1.
x-1.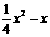 ),
),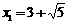 ,
,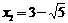 . ∴
. ∴ 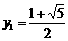 ,
,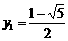 .
.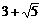 ,
,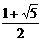 )或(
)或(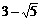 ,
,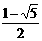 ).
).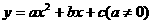 的顶点为M,与
的顶点为M,与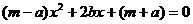 有两个相等的实数根.
有两个相等的实数根.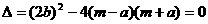 ,得
,得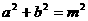
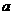 、
、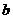 为直角边的等腰直角三角形
为直角边的等腰直角三角形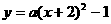
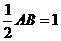 ,即AB=2
,即AB=2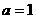
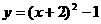 ,即
,即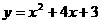
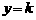
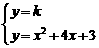
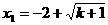 ,
,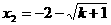 (
(
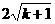
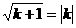
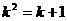
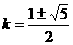
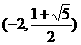 和
和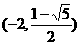
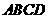 中,
中,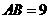 ,
,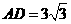 ,点
,点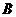 ,点
,点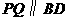 ,交
,交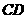 边于
边于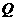 点,再把
点,再把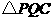 沿着动直线
沿着动直线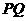 对折,点
对折,点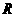 点,设
点,设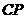 的长度为
的长度为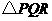 与矩形
与矩形 的度数;
的度数;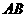 边上?
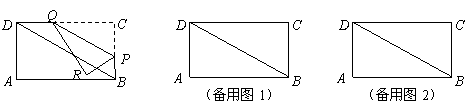
边上?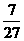 ?
?

 四边形
四边形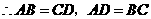 .
.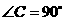 ,
,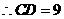 ,
,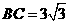 .
.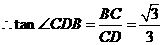 ,
,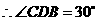 .
.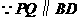 ,
,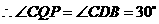 .
.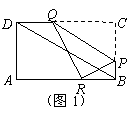 (2)如图1,由轴对称的性质可知,
(2)如图1,由轴对称的性质可知,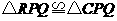 ,
,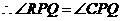 ,
,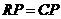 .
.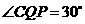 ,
,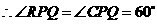 ,
,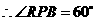 ,
,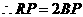 .
.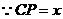 ,
,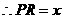 ,
,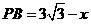 .
.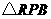 中,根据题意得:
中,根据题意得: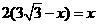 ,
,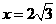 .
.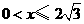 ,
,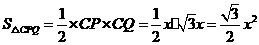 ,
,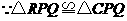 ,
,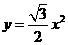
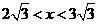 ,
,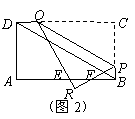 在
在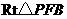 中,
中,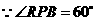 ,
,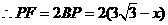 ,
,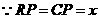 ,
,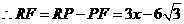 ,
,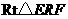 中,
中,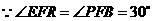 ,
,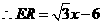 .
.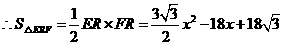 ,
,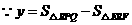 ,
,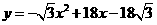 .
.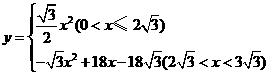 .
.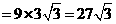 ,当
,当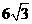 ,而矩形面积的
,而矩形面积的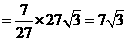 ,
,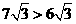 ,所以,当
,所以,当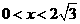 时,
时,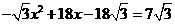 ,解这个方程,得
,解这个方程,得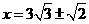 ,因为
,因为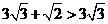 ,
,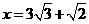 不合题意,舍去.
不合题意,舍去.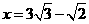 .
.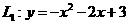 交
交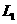 向右平移2个单位后得到抛物线
向右平移2个单位后得到抛物线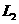 ,
,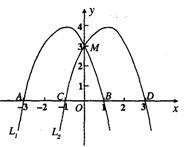


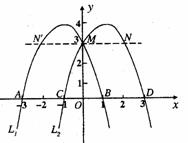

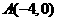 ,
,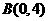 ,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.
,现以A点为位似中心,相似比为9:4,将OB向右侧放大,B点的对应点为C.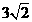 的点P.
的点P.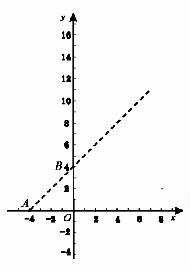
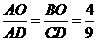 .
.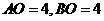 .
.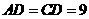 .∴C点坐标为
.∴C点坐标为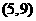 .
.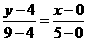
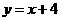
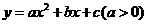 ,由题意得:
,由题意得: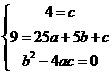 ,
, 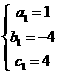
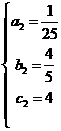
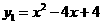 或
或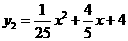 .
.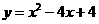
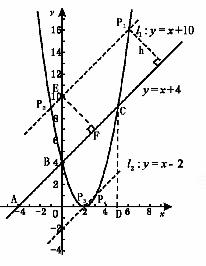
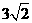 的上下两条平行直线
的上下两条平行直线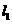 和
和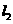 上.
上.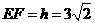 ,
,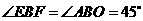 ,
,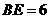 .∴可以求得直线
.∴可以求得直线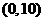
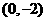
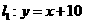 ;
;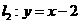 .
.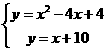 ;⑵
;⑵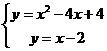
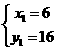 ;
;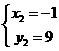 ;
;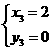 ;
;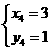
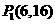 ,
,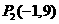 ,
,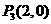 ,
,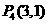 .
.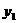 与投资量
与投资量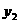 与投资量
与投资量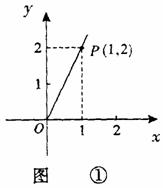
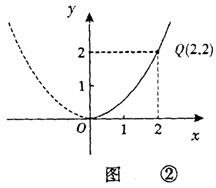
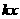 ,由图①所示,函数
,由图①所示,函数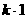 ,
,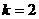
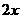 ;
;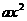 ,由图12-②所示,函数
,由图12-②所示,函数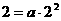 ,
,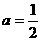
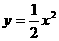 ;
;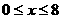 ),
),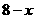 )万元,他获得的利润是
)万元,他获得的利润是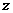 万元,根据题意,得
万元,根据题意,得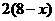 +
+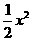 =
=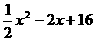 =
=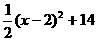
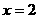 时,
时,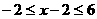
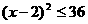
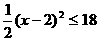
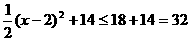 ,即
,即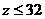 ,此时
,此时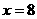
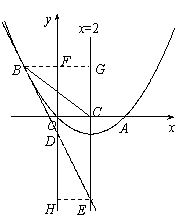
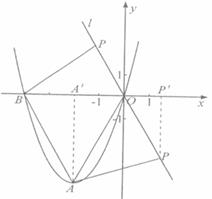
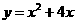 与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.
与x轴分别相交于点B、O,它的顶点为A,连接AB,把AB所的直线沿y轴向上平移,使它经过原点O,得到直线l,设P是直线l上一动点.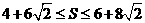 时,求x的取值范围.
时,求x的取值范围. 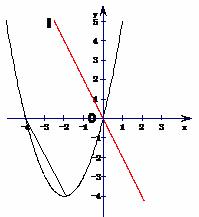
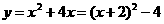
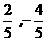 )
)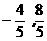 )
)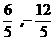 )
)
 的函数关系式是y=-2x
的函数关系式是y=-2x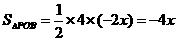
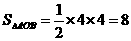 ,
,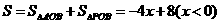
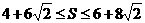 ,
,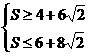
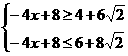 ∴
∴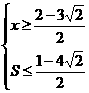
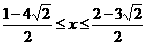
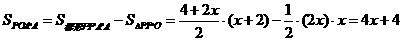
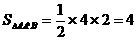
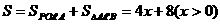
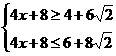 ∴
∴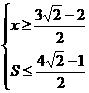
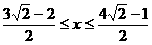
 个单位长度的速度向终点B运动.设运动了x秒.
个单位长度的速度向终点B运动.设运动了x秒.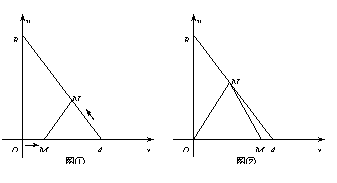

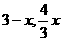 )
)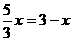 ,
,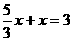 ,
,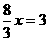 ,
,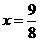
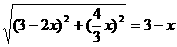
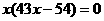
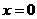 (舍去)或
(舍去)或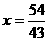
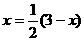 ,
,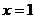
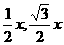 )时,△OMN为正三角形
)时,△OMN为正三角形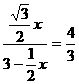 ,解得:
,解得: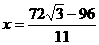
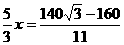
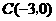 ,点
,点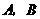 分别在
分别在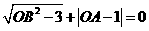 .
.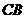 运动,连结
运动,连结 .设
.设 的面积为
的面积为 为顶点的三角形与
为顶点的三角形与 相似?若存在,请直接写出点
相似?若存在,请直接写出点
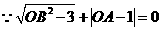
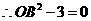 ,
,
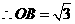 ,
,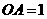
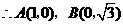
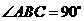
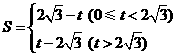
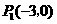 ;
;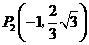 ;
; ;
;