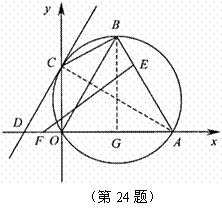
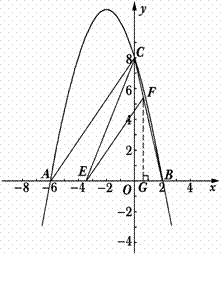
54.(08浙江嘉兴)24.如图,直角坐标系中,已知两点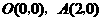 ,点
,点 在第一象限且
在第一象限且 为正三角形,
为正三角形, 的外接圆交
的外接圆交 轴的正半轴于点
轴的正半轴于点 ,过点
,过点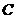 的圆的切线交
的圆的切线交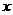 轴于点
轴于点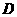 .
.
(1)求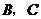 两点的坐标;
两点的坐标;
(2)求直线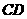 的函数解析式;
的函数解析式;
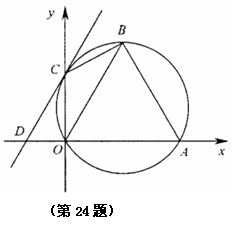
(3)设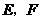 分别是线段
分别是线段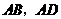 上的两个动点,且
上的两个动点,且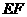 平分四边形
平分四边形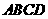 的周长.
的周长.
试探究: 的最大面积?
的最大面积?
(08浙江嘉兴24题解析)24.(1)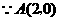 ,
,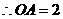 .
.
作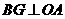 于
于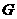 ,
,
 为正三角形,
为正三角形,
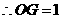 ,
,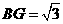 .
.
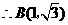 .
.
连 ,
, ,
,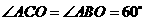 ,
,
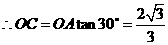 .
.
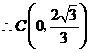 .
.
(2) ,
, 是圆的直径,
是圆的直径,
又 是圆的切线,
是圆的切线,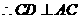 .
.
 ,
,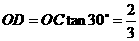 .
.
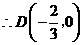 .
.
设直线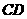 的函数解析式为
的函数解析式为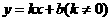 ,
,
则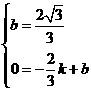 ,解得
,解得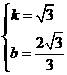 .
.
 直线
直线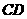 的函数解析式为
的函数解析式为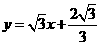 .
.
(3)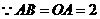 ,
,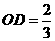 ,
,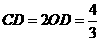 ,
,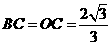 ,
,
 四边形
四边形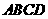 的周长
的周长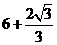 .
.
设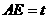 ,
, 的面积为
的面积为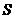 ,
,
则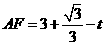 ,
,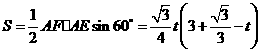 .
.
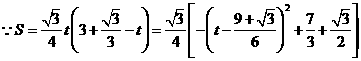 .
.
 当
当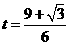 时,
时,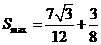 .
.
 点
点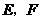 分别在线段
分别在线段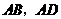 上,
上,
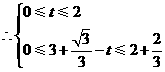 ,解得
,解得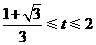 .
.
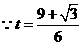 满足
满足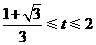 ,
,
 的最大面积为
的最大面积为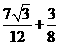 .
.
55(08浙江金华)(本题答案暂缺)24.
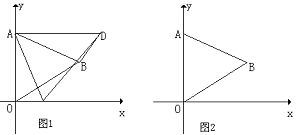
(本题12分) 如图1,在平面直角坐标系中,己知ΔAOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把ΔAOP绕着点A按逆时针方向旋转.使边AO与AB重合.得到ΔABD。(1)求直线AB的解析式;(2)当点P运动到点(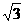 ,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于
,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使ΔOPD的面积等于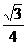 ,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。
,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由。
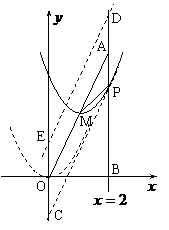
56(08浙江丽水)24.如图,在平面直角坐标系中,已知点 坐标为(2,4),直线
坐标为(2,4),直线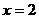 与
与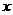 轴相交于点
轴相交于点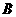 ,连结
,连结 ,抛物线
,抛物线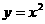 从点
从点 沿
沿 方向平移,与直线
方向平移,与直线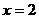 交于点
交于点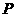 ,顶点
,顶点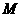 到
到 点时停止移动.
点时停止移动.
 (1)求线段
(1)求线段 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点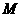 的横坐标为
的横坐标为 ,
,
①用 的代数式表示点
的代数式表示点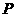 的坐标;
的坐标;
②当 为何值时,线段
为何值时,线段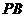 最短;
最短;
(3)当线段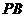 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点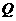 ,使△
,使△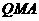
的面积与△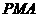 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点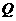 的坐标;若
的坐标;若
不存在,请说明理由.
(08浙江丽水24题解析)24.(本题14分)
解:(1)设 所在直线的函数解析式为
所在直线的函数解析式为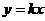 ,
,
∵ (2,4),
(2,4),
∴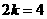 ,
, 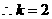 ,
,
∴ 所在直线的函数解析式为
所在直线的函数解析式为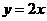 .…………………………………(3分)
.…………………………………(3分)
(2)①∵顶点M的横坐标为 ,且在线段
,且在线段 上移动,
上移动,
∴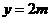 (0≤
(0≤ ≤2).
≤2).
∴顶点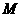 的坐标为(
的坐标为( ,
, ).
).
∴抛物线函数解析式为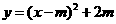 .
.
∴当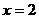 时,
时,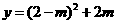
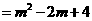 (0≤
(0≤ ≤2).
≤2).
∴点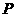 的坐标是(2,
的坐标是(2,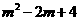 ).…………………………………(3分)
).…………………………………(3分)
② ∵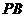 =
=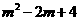 =
=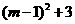 , 又∵0≤
, 又∵0≤ ≤2,
≤2,
∴当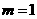 时,PB最短.
……………………………………………(3分)
时,PB最短.
……………………………………………(3分)
(3)当线段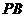 最短时,此时抛物线的解析式为
最短时,此时抛物线的解析式为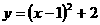 .……………(1分)
.……………(1分)
假设在抛物线上存在点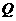 ,使
,使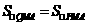 .
.
设点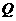 的坐标为(
的坐标为(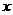 ,
,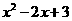 ).
).
①当点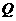 落在直线
落在直线 的下方时,过
的下方时,过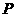 作直线
作直线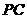 //
// ,交
,交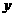 轴于点
轴于点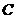 ,
,
∵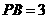 ,
,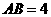 ,
,
∴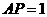 ,∴
,∴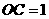 ,∴
,∴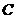 点的坐标是(0,
点的坐标是(0,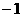 ).
).
 ∵点
∵点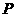 的坐标是(2,3),∴直线
的坐标是(2,3),∴直线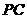 的函数解析式为
的函数解析式为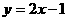 .
.
∵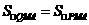 ,∴点
,∴点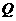 落在直线
落在直线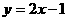 上.
上.
∴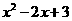 =
=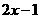 .
.
解得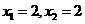 ,即点
,即点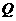 (2,3).
(2,3).
∴点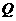 与点
与点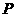 重合.
重合.
∴此时抛物线上不存在点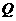 ,使△
,使△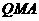 与
与
△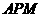 的面积相等.………………………(2分)
的面积相等.………………………(2分)
②当点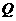 落在直线
落在直线 的上方时,
的上方时,
作点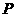 关于点
关于点 的对称称点
的对称称点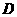 ,过
,过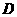 作直线
作直线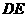 //
// ,交
,交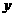 轴于点
轴于点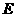 ,
,
∵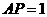 ,∴
,∴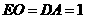 ,∴
,∴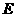 、
、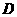 的坐标分别是(0,1),(2,5),
的坐标分别是(0,1),(2,5),
∴直线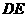 函数解析式为
函数解析式为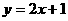 .
.
∵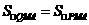 ,∴点
,∴点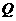 落在直线
落在直线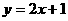 上.
上.
∴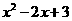 =
=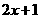 .
.
解得: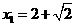 ,
,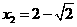 .
.
代入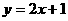 ,得
,得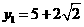 ,
,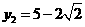 .
.
∴此时抛物线上存在点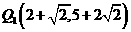 ,
,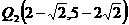
使△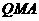 与△
与△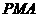 的面积相等. …………………………………(2分)
的面积相等. …………………………………(2分)
综上所述,抛物线上存在点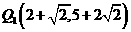 ,
,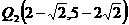
使△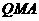 与△
与△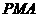 的面积相等.
的面积相等.
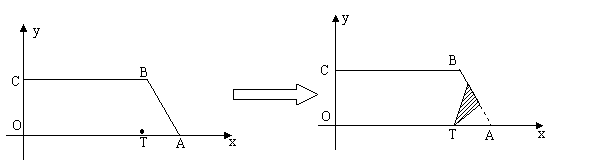
57(08浙江衢州)24、(本题14分)已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),A(10,0),B(8,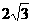 ),C(0,
),C(0,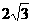 ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;
(2)当纸片重叠部分的图形是四边形时,求t的取值范围;
(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由。
(08浙江衢州24题解析)24、(本题14分)
解:(1) ∵A,B两点的坐标分别是A(10,0)和B(8,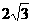 ),
),
∴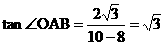 ,
,
∴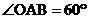
当点A´在线段AB上时,∵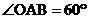 ,TA=TA´,
,TA=TA´,
∴△A´TA是等边三角形,且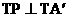 ,
,
∴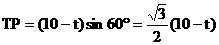 ,
,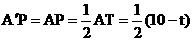 ,
,
|
|
|
 ∴
∴ ,
,
|
|
|
|
|
|
|
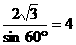 ,
,
所以此时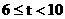 。
。
(2)当点A´在线段AB的延长线,且点P在线段AB(不与B重合)上时,
纸片重叠部分的图形是四边形(如图(1),其中E是TA´与CB的交点),
|
|
|
 当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
当点P与B重合时,AT=2AB=8,点T的坐标是(2,0)
又由(1)中求得当A´与B重合时,T的坐标是(6,0)
|
|
|
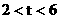 。
。
|
|
|
|
|
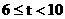 时,
时,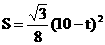 ,
,
在对称轴t=10的左边,S的值随着t的增大而减小,
∴当t=6时,S的值最大是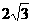 。
。
2当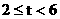 时,由图1,重叠部分的面积
时,由图1,重叠部分的面积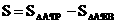
∵△A´EB的高是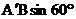 ,
,
∴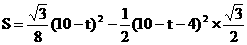
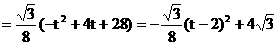
当t=2时,S的值最大是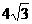 ;
;
3当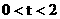 ,即当点A´和点P都在线段AB的延长线是(如图2,其中E是TA´与CB的交点,F是TP与CB的交点),
,即当点A´和点P都在线段AB的延长线是(如图2,其中E是TA´与CB的交点,F是TP与CB的交点),
∵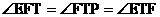 ,四边形ETAB是等腰形,∴EF=ET=AB=4,
,四边形ETAB是等腰形,∴EF=ET=AB=4,
∴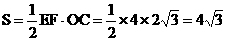
综上所述,S的最大值是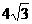 ,此时t的值是
,此时t的值是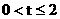 。
。
58(08浙江绍兴)24.将一矩形纸片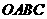 放在平面直角坐标系中,
放在平面直角坐标系中,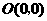 ,
,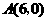 ,
,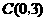 .动点
.动点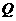 从点
从点 出发以每秒1个单位长的速度沿
出发以每秒1个单位长的速度沿 向终点
向终点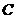 运动,运动
运动,运动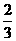 秒时,动点
秒时,动点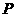 从点
从点 出发以相等的速度沿
出发以相等的速度沿 向终点
向终点 运动.当其中一点到达终点时,另一点也停止运动.设点
运动.当其中一点到达终点时,另一点也停止运动.设点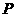 的运动时间为
的运动时间为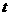 (秒).
(秒).
(1)用含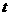 的代数式表示
的代数式表示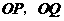 ;
;
(2)当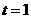 时,如图1,将
时,如图1,将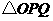 沿
沿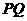 翻折,点
翻折,点 恰好落在
恰好落在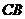 边上的点
边上的点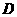 处,求点
处,求点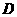 的坐标;
的坐标;
(3)连结 ,将
,将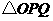 沿
沿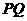 翻折,得到
翻折,得到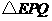 ,如图2.问:
,如图2.问: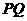 与
与 能否平行?
能否平行?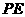 与
与 能否垂直?若能,求出相应的
能否垂直?若能,求出相应的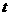 值;若不能,说明理由.
值;若不能,说明理由.

(08浙江绍兴24题解析)24.(本题满分14分)
解:(1) ,
,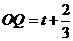 .
.

(2)当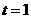 时,过
时,过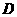 点作
点作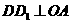 ,交
,交 于
于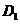 ,如图1,
,如图1,
则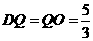 ,
,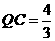 ,
,
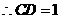 ,
,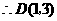 .
.
(3)①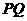 能与
能与 平行.
平行.
若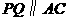 ,如图2,则
,如图2,则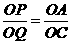 ,
,
即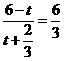 ,
,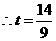 ,而
,而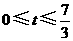 ,
,
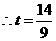 .
.
②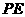 不能与
不能与 垂直.
垂直.
若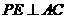 ,延长
,延长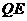 交
交 于
于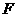 ,如图3,
,如图3,
则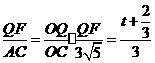 .
.
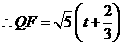 .
.
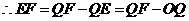
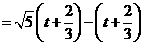
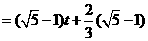 .
.
又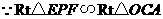 ,
,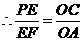 ,
,
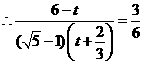 ,
,
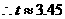 ,而
,而 ,
,
 不存在.
不存在.
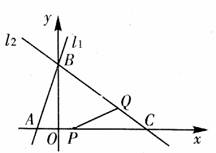 (08山西省卷)(本题答案暂缺)26.(本题14分)如图,已知直线
(08山西省卷)(本题答案暂缺)26.(本题14分)如图,已知直线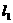 的解析式为
的解析式为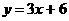 ,直线
,直线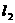 经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线
经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线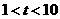 )。
)。 中,直线
中,直线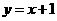 与
与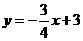 交于点
交于点 ,分别交
,分别交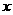 轴于点
轴于点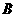 和点
和点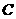 ,点
,点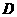 是直线
是直线 上的一个动点.
上的一个动点.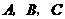 的坐标.
的坐标. 为等腰三角形时,求点
为等腰三角形时,求点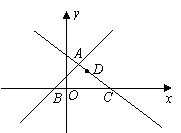 (3)在直线
(3)在直线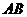 上是否存在点
上是否存在点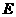 ,使得以点
,使得以点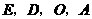 为顶点的四边形是平行四边形?如果存在,直线写出
为顶点的四边形是平行四边形?如果存在,直线写出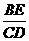 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.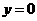 时,
时,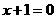 ,
,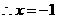 ,点
,点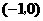 .·········································································· 1分
.·········································································· 1分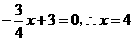 ,点
,点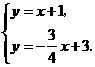 解得
解得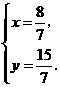
 点
点 .····················································································· 3分
.····················································································· 3分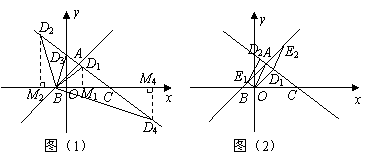 (2)当
(2)当 .
.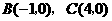 ,
,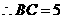 .
.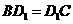 时,过点
时,过点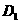 作
作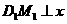 轴,垂足为点
轴,垂足为点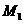 ,则
,则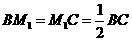 .
.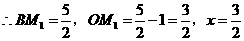 .
.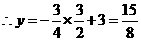 ,点
,点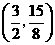 .················································· 4分
.················································· 4分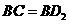 时,过点
时,过点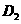 作
作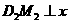 轴,垂足为点
轴,垂足为点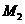 ,则
,则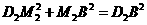 .
.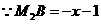 ,
,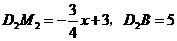 ,
,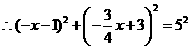 .
.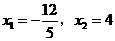 (舍去).此时,
(舍去).此时,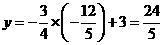 .
.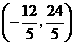 .·············································································· 6分
.·············································································· 6分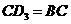 ,或
,或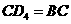 时,同理可得
时,同理可得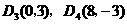 .····················· 9分
.····················· 9分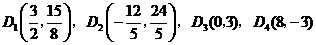 .
.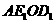 为平行四边形时,
为平行四边形时,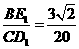 .··········································· 10分
.··········································· 10分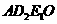 为平行四边形时,
为平行四边形时,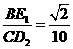 .············································ 11分
.············································ 11分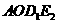 为平行四边形时,
为平行四边形时,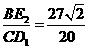 .········································ 12分
.········································ 12分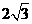 km处。
km处。
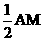 。
。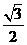 =3,ME=
=3,ME=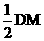 =
=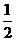 ×
×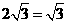 ,
,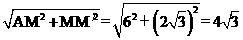 ………(7分)
………(7分)
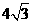 …………(10分)
…………(10分) 在线段AB上任取一点G′,过G′作G′N′⊥OE于N′点,
在线段AB上任取一点G′,过G′作G′N′⊥OE于N′点, .将直线
.将直线 0),直角梯形OABC被直线
0),直角梯形OABC被直线 ,
, 时,求S关于
时,求S关于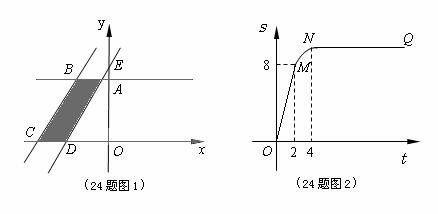 (2)在第(1)题的条件下,当直线
(2)在第(1)题的条件下,当直线 为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
为等腰直角三角形?若存在,请直接写出所有满足条件的点P的坐标;若不存在,请说明理由. ,正方形
,正方形 顶点
顶点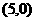 ,顶点
,顶点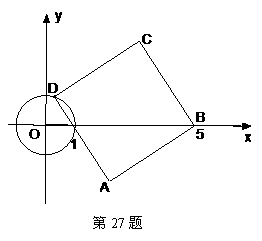 (3)设点
(3)设点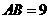 ,
,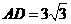 ,点
,点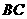 上的动点(点
上的动点(点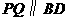 ,交
,交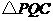 沿着动直线
沿着动直线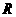 点,设
点,设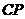 的长度为
的长度为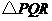 与矩形
与矩形 的度数;
的度数; 边上?
边上? ?
?
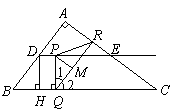
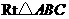 中,
中,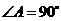 ,
,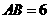 ,
,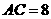 ,
,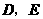 分别是边
分别是边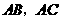 的中点,点
的中点,点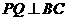 于
于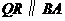 交
交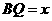 ,
,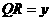 .
.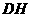 的长;
的长;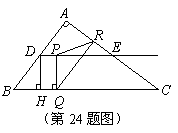 (3)是否存在点
(3)是否存在点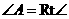 ,
,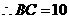 .
.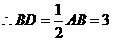 .
.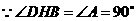 ,
,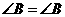 .
.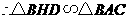 ,
,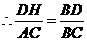 ,
,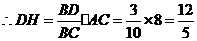 .
.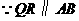 ,
,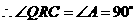 .
.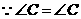 ,
,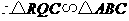 ,
,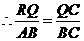 ,
,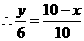 ,
,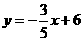 .
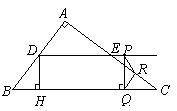
. ①当
①当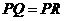 时,过点
时,过点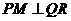 于
于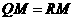 .
.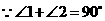 ,
,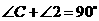 ,
,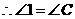 .
.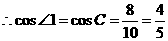 ,
,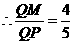 ,
,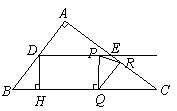
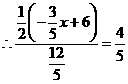 ,
,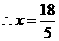 .
. ②当
②当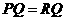 时,
时,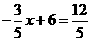 ,
,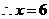 .
.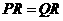 时,则
时,则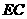 的中点,
的中点,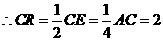 .
.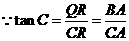 ,
,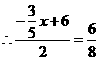 ,
,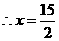 .
.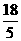 或6或
或6或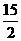 时,
时,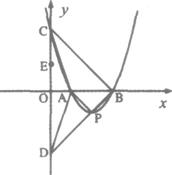
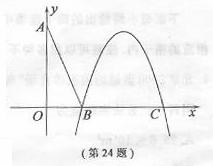
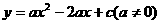 与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0)。
与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0)。 (3)若平行于x轴的动直线
(3)若平行于x轴的动直线 中,
中, ,
,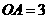 .分别以
.分别以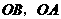 所在直线为
所在直线为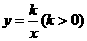 的图象与
的图象与 与
与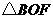 的面积相等;
的面积相等;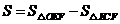 ,求当
,求当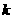 为何值时,
为何值时, 沿
沿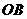 上?若存在,求出点
上?若存在,求出点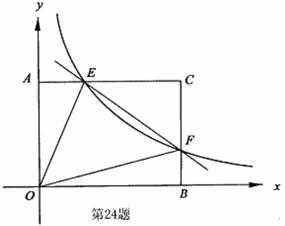
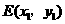 ,
,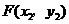 ,
,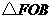 的面积分别为
的面积分别为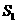 ,
,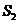 ,
,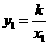 ,
,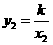 .
.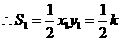 ,
,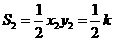 .
.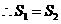 ,即
,即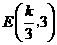 ,
,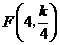 ,
,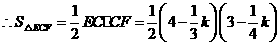 ,
,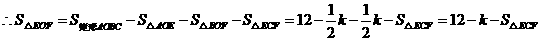
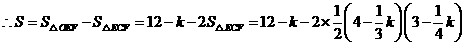
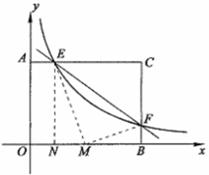
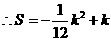 .
.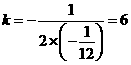 时,
时,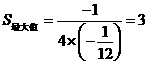 .
.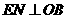 ,垂足为
,垂足为 .
.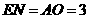 ,
,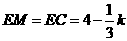 ,
,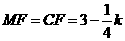 ,
,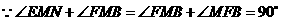 ,
,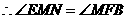 .
.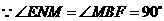 ,
,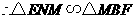 .
.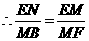 ,
,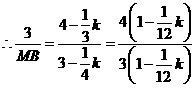 ,
,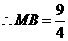 .
.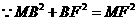 ,
,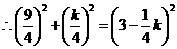 ,解得
,解得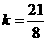 .
.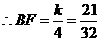 .
.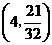 .
.

 (08浙江杭州24) 在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二次函数
(08浙江杭州24) 在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二次函数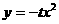 的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。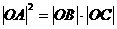 ?请你作出判断,并说明理由;
?请你作出判断,并说明理由;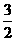 ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。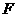 的顶点为
的顶点为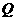 ,
,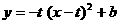 .
--- 2分
.
--- 2分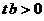 .
--- 1分
.
--- 1分 , 得
, 得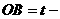
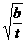 ,
,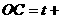

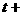
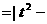
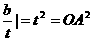 ,
,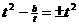 , 所以当
, 所以当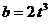 时, 存在抛物线
时, 存在抛物线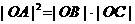 .-- 2分
.-- 2分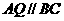 , ∴
, ∴ 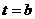 ,
得
,
得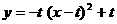 ,
,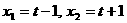 .
--- 1分
.
--- 1分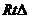
 中,
中,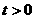 时,由
时,由 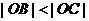 , 得
, 得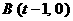 ,
, 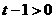 时, 由
时, 由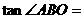
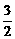
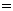
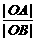
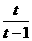 , 解得
, 解得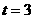 ,
, 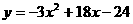 ;
--- 2分
;
--- 2分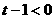 时, 由
时, 由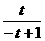 , 解得
, 解得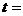
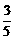 ,
, 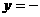
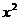 +
+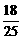
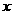 +
+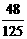 .
--- 2分
.
--- 2分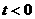 时, 由
时, 由 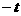 代
代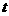 , 可得
, 可得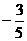 ,
, 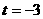 ,
,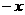 代
代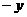 代
代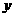 得到)
得到)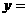
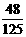 或
或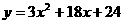 . ---
2分.
. ---
2分.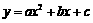 (a≠0),顶点C (1,
(a≠0),顶点C (1,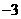 ),与x轴交于A、B两点,
),与x轴交于A、B两点,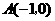 .
.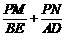 是否为定值?
若是,请求出此定值;若不是,请说明理由.
是否为定值?
若是,请求出此定值;若不是,请说明理由.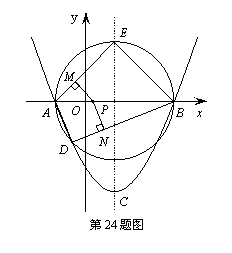 (3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP ,FG分别与边AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断
(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP ,FG分别与边AE、BE相交于点F、G(F与A、E不重合,G与E、B不重合),请判断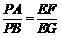 是否成立.若成立,请给出证明;若不成立,请说明理由.
是否成立.若成立,请给出证明;若不成立,请说明理由.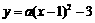 .......... 1分
.......... 1分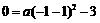 ∴
∴ 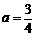 ..................................... 2分
..................................... 2分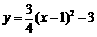 ,即:
,即: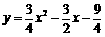 ......................... 3分
......................... 3分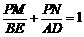 ........................................................................... 4分
........................................................................... 4分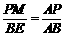 ①
①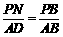 ② .................................................................................. 5分
② .................................................................................. 5分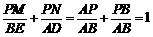 .................................................................. 6分
.................................................................. 6分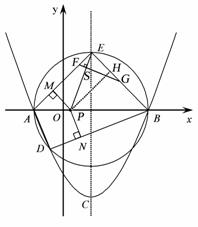 如图,过点P作PH⊥BE于H,
如图,过点P作PH⊥BE于H,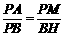
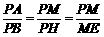 ①.................. 8分
①.................. 8分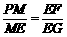 ②
②