2.结论开放与探索
给出问题的条件,让解题者根据条件探索相应的结论,并且符合条件的结论往往呈现多样性,或者相应的结论的“存在性”需要解题者进行推断,甚至要求解题者探求条件在变化中的结论,这些问题都是结论开放性问题。它要求解题者充分利用条件进行大胆而合理的猜想,发现规律,得出结论,这类题主要考查解题者的发散性思维和所学基本知识的应用能力。
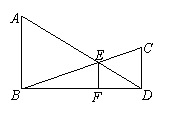
[例1] (吉林省中考题)将两块完全相同的等腰直角三角形摆成如图的样子,假设图形中的所有点、线都在同一平面内,
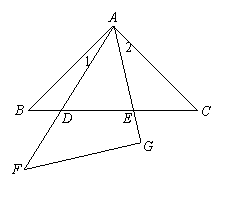 回答下列问题:
回答下列问题:
⑴图中共有多少个三角形?把它们一
一写出来;
⑵图中有相似(不包括全等)三角形
吗?如果有,就把它们一一写出来。
[解析]:⑴先看△ABC中,一一数来共有6个三
角形,再加上△AFG,共七个三角形;⑵由于∠DAE
=∠B=∠C=45°,∠ADE=∠B+∠1=45°+∠1=∠BAE,同理∠AED=∠CAD,可得出△ADE∽△BAE∽△CDA。
⑴共有七个三角形,它们是:
△ABD、△ABE、△ABC、△ADE、△ADC、△AEC、△AFG。
⑵有相似三角形,它们是:
△ADE∽△BAE,△BAE∽△CDA,△ADE∽△CDA(或△ADE∽△BAE∽△CDA)。
[评注]:本题为考生提供了广阔的探究空间,通过分析、判断,有利于学生创新意识的形成和思维能力的培养。
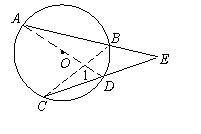
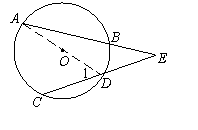
[例2] 如图,⊙O的弦AB、CD的延长线相交于点E。请你根据上述条件,
写出一个正确的结论(所写的结论不能自行再添加新的线段及标注其他字母),并给出证明(证明时允许自行添加辅助线)。
|
|
①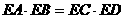 ;②AC>BC;③AE>DE;……
;②AC>BC;③AE>DE;……
可以得出的结论及证明如下:
①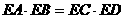
如图连结AD、BC,∵∠A=∠C,∠E=∠E,
|
|
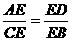 ,即
,即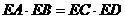
②AC>BC;
如图,连结AD,
|
|

|
|
∴AC>BC;
③AE>DE。
证法一:如图,连结AD、BD、BC。
∵∠2是△BCD的外角,∠C是△BCD的内角,
∴∠2>∠C。而∠ADE>∠2,∠C>∠A,
∴在△ADE中,∠ADE>∠A。∴AE>DE
证法二:∵EA·EB<EA2,ED·EC>ED2,
而EA·EB =ED·EC ∴EA2>ED2,即EA>ED。
[评注]:这是一道以探索结论为目的的开放型试题,它不限结论,而是让考生根据条件去探索结论。因此,这类考题对开阔视野、启迪智慧、培养发散思维能力大有好处。
[例3] (北京市东城区中考题)有一个二次函数的图象,三位学生分别说出它们的一些特点:
甲:对称轴是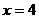 ;
;
乙:与 轴两个交点的横坐标都是整数;
轴两个交点的横坐标都是整数;
丙:与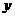 轴交点的纵坐标也是整数,且以三个交点为顶点的三角形面积为3。
轴交点的纵坐标也是整数,且以三个交点为顶点的三角形面积为3。
请你写出满足上述全部特点的一个二次函数的解析式:___________________。
[解析]:此题是一道结论开放型试题,题目条件已确定,而所要求的结论不惟一。本题以二次函数基本知识的掌握,同时也考查了学生发散思维的能力和数形结合的思想。由二次函数图象的对称性及已知条件不难分析得出,若与 轴两个交点的坐标分别是(3,0),(5,0),则与
轴两个交点的坐标分别是(3,0),(5,0),则与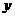 轴交点为(0,3)或(0,
轴交点为(0,3)或(0,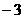 ),此时二次函数的解析式为
),此时二次函数的解析式为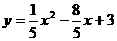 或
或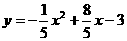 ;若与
;若与 轴两个交点的坐标分别是(1,0),(7,0),则与
轴两个交点的坐标分别是(1,0),(7,0),则与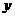 轴交点为(0,1)或(0,
轴交点为(0,1)或(0,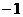 ),此时二次函数的解析式为
),此时二次函数的解析式为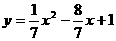 或
或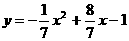 ,只要得出一个答案即可。
,只要得出一个答案即可。
[例4] 关于 的方程
的方程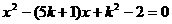 ,是否存在负数
,是否存在负数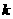 ,使方程的两个实数根的倒数和等于4?若存在,求出满足条件的
,使方程的两个实数根的倒数和等于4?若存在,求出满足条件的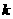 的值;若不存在,说明理由。
的值;若不存在,说明理由。
[解析]:先假设存在有满足条件的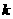 值,利用一元二次方程根与系数的关系,结合题意得出关于
值,利用一元二次方程根与系数的关系,结合题意得出关于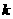 的方程。若能求出符合题意的
的方程。若能求出符合题意的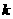 值,则
值,则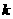 存在,否则
存在,否则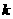 不存在。
不存在。
设方程的两个实数根是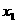 ,
,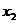 ,由根与系数的关系,得
,由根与系数的关系,得
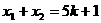 ,
,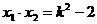
由题意得 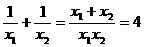 。
。
∴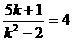 ∴
∴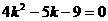
又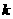 <0, ∴
<0, ∴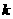 =
=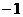 ,此时△=20>0成立, ∴
,此时△=20>0成立, ∴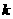 =
=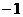 。
。
[例5] (淮安市中考题)在平面直角坐标系 O
O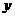 中,已知抛物线
中,已知抛物线
 的对称轴为
的对称轴为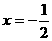 ,设抛物线与
,设抛物线与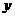 轴交于A点,与
轴交于A点,与 轴交于B、C两点(B点在C点的左边),锐角△ABC的高BE交AO于点H。
轴交于B、C两点(B点在C点的左边),锐角△ABC的高BE交AO于点H。
⑴求抛物线的解析式;
⑵在⑴中抛物线上是否存在点P,使BP将△ABH的面积分成1∶3两部分?如果存在,求出P点的坐标;如果不存在,请说明理由。
[解析]:⑴略;⑵解本题的方法是先假设这样的抛物线存在,然后根据题中的条件进行求解。
⑴抛物线的解析式为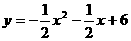 ;
;
⑵令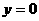 ,即
,即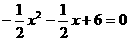 ,得
,得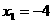 ,
,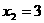 ∴A(0,6),B(
∴A(0,6),B(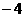 ,0),C(3,0),由题意,有Rt△BHO∽Rt△ACO,得
,0),C(3,0),由题意,有Rt△BHO∽Rt△ACO,得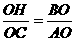 ,即
,即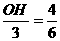 ,
,
∴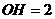 ,故
,故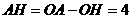 。
。
假设在抛物线上存在点P,使BP将△ABH的面积分成1∶3两部分,则BP必过点(0,5)或(0,3)。
当BP过点(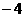 ,0)和(0,5)时,设BP的解析式为
,0)和(0,5)时,设BP的解析式为
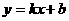 ,则
,则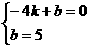 ,解得
,解得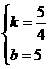
∴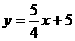 。由
。由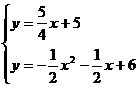 解得
解得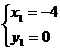 ,
,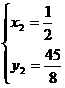 ,∴P点坐标为(
,∴P点坐标为(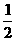 ,
,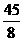 )
)
当BP过点(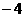 ,0)和(0,3)时,设BP的解析式为
,0)和(0,3)时,设BP的解析式为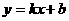 ,则
,则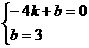 ,解得
,解得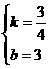
∴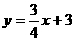 。由
。由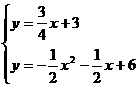 解得
解得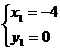 ,
,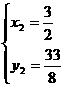 , ∴P点坐标为(
, ∴P点坐标为(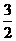 ,
,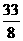 )
)
故抛物线上存在两点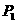 (
(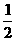 ,
,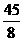 ),
),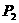 (
(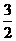 ,
,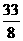 ),使BP分△ABH的面积为1∶3。
),使BP分△ABH的面积为1∶3。
[评注]:探索存在性问题的基本思路是,可先假设结论存在或成立,以此为前提进行运算或推理,若推出矛盾可否定假设,否则给出肯定的证明。
[例6] (湖北黄冈中考题)已知:如图,AB⊥CD,CD⊥BD,
 垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,
垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,
我们可以证明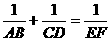 成立(不要求考生证明)。
成立(不要求考生证明)。
若将图中的垂直改为斜交,如图,AB∥CD,AD、BC
相交于点E,过点E作EF∥AB,交BD于点F,则:
⑴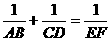 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
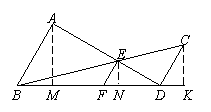 ⑵请找出S△ABD、S△BCD和S△BED间的关系式,并给出证明。
⑵请找出S△ABD、S△BCD和S△BED间的关系式,并给出证明。
[解析]:右图所表示的是一般情况,在探索结论的过程中,应
设法将之转化为上图这样的特殊情况,故可过A、E、C点
作BD的垂线。
⑴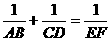 仍成立。
仍成立。
证明:过点A、E、C点作BD的垂线,交BD或其延长线于点M、N、K。
易证Rt△ABM∽Rt△EFN∽Rt△CDK。
∴AB∶EF∶CD=AM∶EN∶CK。
由题设 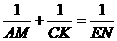 ,知
,知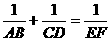 成立。
成立。
⑵由题设 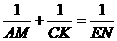 ,
,
∴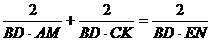 ;
;
即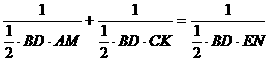 ;
;
又 ∵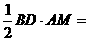 S△ABD ,
S△ABD ,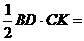 S△BCD ,
S△BCD ,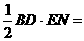 S△BED 。
S△BED 。
∴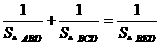 。
。
[评注]:本题从特殊情形入手,通过图形的变换,寻找数量上的内在规律,颇具新意。
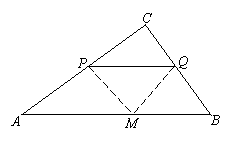
[例7] (福州市中考题)已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC上(与点A、C不重合),Q点在BC上。
⑴当△PQC的面积与四边形PABQ的面积相等时,求CP的长;
⑵当△PQC的周长与四边形PABQ的周长相等时,求CP的长;
试问,在AB上是否存在点M,使得△PQM为等腰直角三角形?若不存在,请说明理由;若存在,请求出PQ的长;
[解析]:本题是纯几何探索性问题,解这类题时,是先假设结论存在。若从已知条件和定义、定理出发,进行推理或计算得出相应的结论,则结论确实存在;若推证出矛盾或计算无解,则结论不存在。
⑴、⑵略。
⑶如图,△PQM为等腰直角三角形可能有两种情况:
①由右图假设,∠MPN=90°,PM=PQ时,由勾股定理逆定理则得∠C=90°。
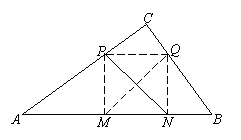 ∴△ABC的AB上的高为
∴△ABC的AB上的高为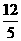 。
。
设PM=PQ= ,∵PQ∥AB,∴△CPQ∽△CAB。
,∵PQ∥AB,∴△CPQ∽△CAB。
∴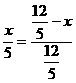 ,解之得
,解之得 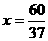 ,即
,即 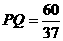 。
。
 当∠MQ′P=90°,QP=QM′时,同理得
当∠MQ′P=90°,QP=QM′时,同理得 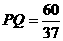 。
。
②由右图,假设∠PMQ=90°,MP=MQ时,
M到PQ的距离为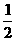 PQ。
PQ。
设PQ= ,∵PQ∥AB,∴△CPQ∽△CAB。
,∵PQ∥AB,∴△CPQ∽△CAB。
∴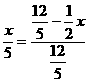 ,解之得
,解之得 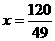 ,即
,即 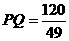 。
。
∴综上所述,在AB上存在点M,使△PQM为等腰直角三角形。
 [评注]:“存在性”探索题,往往与传统的综合题相结合,来加大对考生分析、探索能力的考查,这类问题的情景新颖,富有挑战性,是启迪智慧的好素材。
[评注]:“存在性”探索题,往往与传统的综合题相结合,来加大对考生分析、探索能力的考查,这类问题的情景新颖,富有挑战性,是启迪智慧的好素材。
[题型设计与能力训练]
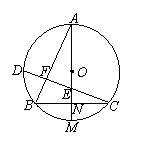 (重庆市中考题)如图,AM是⊙O的直径,过⊙O上一点B作BN⊥AM,垂足为N,其延长线交⊙O于点C,弦CD交AM于点E。
(重庆市中考题)如图,AM是⊙O的直径,过⊙O上一点B作BN⊥AM,垂足为N,其延长线交⊙O于点C,弦CD交AM于点E。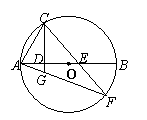 (辽宁省中考题)已知:如图,AB是⊙O的直径,C是⊙O上一点,连结AC,过C点作直线CD⊥AB于D(AD<DB),点E是DB上任意
(辽宁省中考题)已知:如图,AB是⊙O的直径,C是⊙O上一点,连结AC,过C点作直线CD⊥AB于D(AD<DB),点E是DB上任意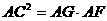 ;
;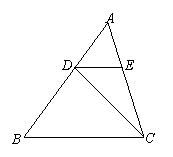 (福建福州市中考题)如图,已知△ABC中,AB=4,D在AB边上移动(不与A、B重合),DE∥BC交AC于E,连结CD。设S△ABC=S,S△DEC=S1。
(福建福州市中考题)如图,已知△ABC中,AB=4,D在AB边上移动(不与A、B重合),DE∥BC交AC于E,连结CD。设S△ABC=S,S△DEC=S1。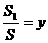 ,求
,求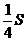 成立?
成立?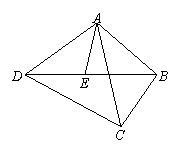 ⑴求证:
⑴求证: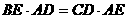 ;
;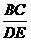 可能等于哪两条线段
可能等于哪两条线段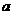 ,竖直方向的边长均为
,竖直方向的边长均为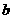 ):
):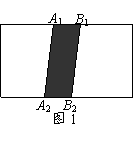



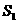 =_________,
=_________,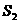 =_________,
=_________,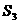 =__________;
=__________;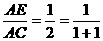 时,有
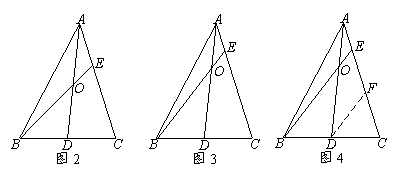
时,有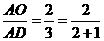 (如图1);
(如图1);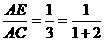 时,有
时,有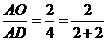 (如图2);
(如图2);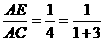 时,有
时,有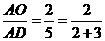 (如图3);
(如图3);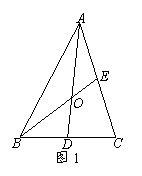
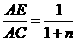 时,参照上述研究结论,请你猜想用
时,参照上述研究结论,请你猜想用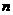 表示
表示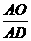 的一般结论,并给出证明(其中
的一般结论,并给出证明(其中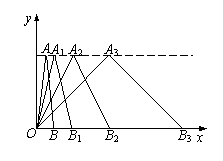 △OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第
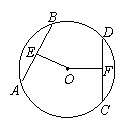
△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第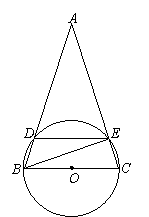 心距,如果OE=OF,那么____________(只需写出一个正确的结论)。
心距,如果OE=OF,那么____________(只需写出一个正确的结论)。