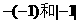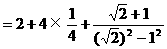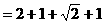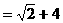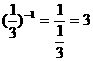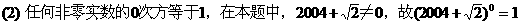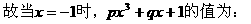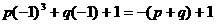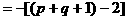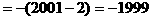0 47852 47860 47866 47870 47876 47878 47882 47888 47890 47896 47902 47906 47908 47912 47918 47920 47926 47930 47932 47936 47938 47942 47944 47946 47947 47948 47950 47951 47952 47954 47956 47960 47962 47966 47968 47972 47978 47980 47986 47990 47992 47996 48002 48008 48010 48016 48020 48022 48028 48032 48038 48046 447348
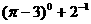 的结果为:
的结果为: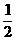 B.
-2 C.
B.
-2 C. 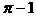 D.
D.
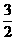
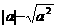 的结果正确的是_________
的结果正确的是_________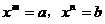 ,(其中x≠0,m、n为正整数),则
,(其中x≠0,m、n为正整数),则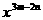 的值等于______
的值等于______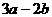 B.
B.
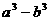 C.
C.
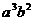 D.
D.
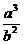
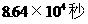 B.
B. 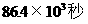 C.
C. 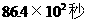 D.
D.
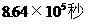
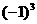 和1 B.
和1 B. 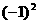 和-1 C.
和-1 C. 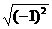 和-1 D.
和-1 D.