0 47949 47957 47963 47967 47973 47975 47979 47985 47987 47993 47999 48003 48005 48009 48015 48017 48023 48027 48029 48033 48035 48039 48041 48043 48044 48045 48047 48048 48049 48051 48053 48057 48059 48063 48065 48069 48075 48077 48083 48087 48089 48093 48099 48105 48107 48113 48117 48119 48125 48129 48135 48143 447348
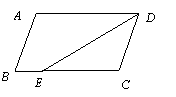

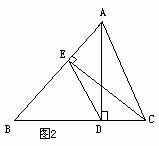 分析:首先凸显△BAD和△BCE,可证明相似,即可得到比例式
分析:首先凸显△BAD和△BCE,可证明相似,即可得到比例式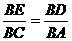 ,进而再凸显△BDE和△BAC,可根据两边对应成比例且夹角相等,两三角形相似.
,进而再凸显△BDE和△BAC,可根据两边对应成比例且夹角相等,两三角形相似.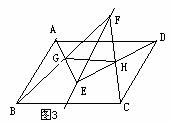 分析:本例如何探寻“中间比”来过渡“
分析:本例如何探寻“中间比”来过渡“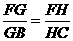 ”是证题的关键,可分别凸显△BAG和△FEG,△DCH和△EFH,即可得“中间比
”是证题的关键,可分别凸显△BAG和△FEG,△DCH和△EFH,即可得“中间比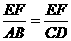 ”
”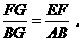
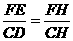 .
. .
.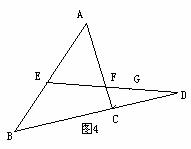
 ∴△BAG∽△FEG,△DCH∽△EFH……(凸显思想的体现)
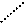
∴△BAG∽△FEG,△DCH∽△EFH……(凸显思想的体现)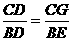 ,
,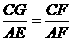
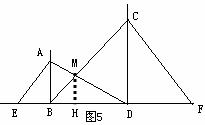 离地面的高MH.
离地面的高MH.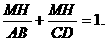
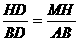 ①,
①,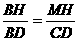 ②
②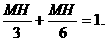
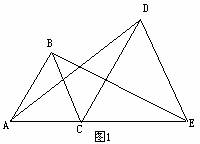 在△ACD和△BCE中
在△ACD和△BCE中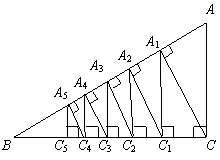 如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作
如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作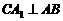 ,垂足为
,垂足为 ,再过
,再过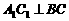 ,垂足为
,垂足为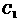 ;过
;过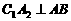 ,垂足为
,垂足为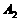 ,再过
,再过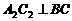 ,垂足为
,垂足为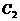 ;……,这样一直做下去,得到一组线段
;……,这样一直做下去,得到一组线段 ,
, ,
,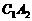 ,……,则第10条线段
,……,则第10条线段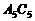 =_______________.
=_______________.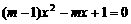 一两个不相等的实数根,则m的取值范围是_______________________.
一两个不相等的实数根,则m的取值范围是_______________________.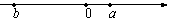 已知实数a、b在数轴上的位置如图所示,则以下三个命题:(1)
已知实数a、b在数轴上的位置如图所示,则以下三个命题:(1)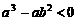 ,(2)
,(2)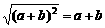 ,(3)
,(3)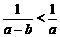 ,其中真命题的序号为_________________.
,其中真命题的序号为_________________.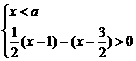 的解集为
的解集为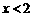 ,则a的取值范围是_____________.
,则a的取值范围是_____________.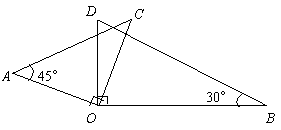 将一副直角三角板按图示方法放置(直角顶点重合),则
将一副直角三角板按图示方法放置(直角顶点重合),则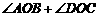 =____.
=____.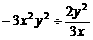 =__________.
=__________.