例17(2004 哈尔滨)中小学生的视力状况受到全社会的广泛关注,某市有关部门对全市4万名初中生的视力状况进行一次抽样调查统计,所得到的有关数据绘制成频率分布直方图,如下图,从左至右五个小组的频率之比依次是2:4:9:7:3,第五小组的频数是30.
(1)本次调查共抽测了多少名学生?
(2)本次调查抽测的数据的中位数应在哪个小组?说明理由.
(3)如果视力在4.9-5.1(含4.9、5.1)均属正常,那么全市初中生视力正常的约有多少人?
解:(1)因为频率之比等于频数之比,
设第一小组的频数为2k,所以各组的频数依次为2k、4k、9k、7k、3k,
于是3k=30,所以k=10
所以2k=20,4k=40,9k=90,7k=70,所以20+40+90+70+30=250(人).
答:本次调查共抽测了250名学生.
(2)中位数应在第三小组.
∵250个数据的中位数是第125和第126两个数据的平均数,
前两个小组的频数之和是20+40=60,60<125
 第三小组的频数是90,90+60=150,150>126,
第三小组的频数是90,90+60=150,150>126,
∴中位数应在第三小组.
(3)∵视力在4.9-5.1范围内的人有70人,
∴频率=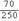 =0.28,
=0.28,
∴全市初中生视力正常的约有40000×0.28=11200(人),
答:全市初中生视力正常的约有11200人.
例18、(2004河北)为了普及环保知识,增强环保意识,某中学组织了环保知识竞赛活动,
初中三各年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
|
|
决赛成绩(单位:分) |
|
初一年级 |
80 86 88 80 88 99 80 74 91 89 |
|
初二年级 |
85 85 87 97 85 76 88 77 87 88 |
|
初三年级 |
82 80 78 78 81 96 97 88 89 86 |
(1)请你填写下表:
|
|
平均分 |
众数 |
中位数 |
|
初一年级 |
85.5 |
|
87 |
|
初二年级 |
85.5 |
85 |
|
|
初三年级 |
|
|
84 |
(2)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
①从众数和平均数相结合看(分析哪个年级成绩好些);
②从平均数和中位数相结合看(分析哪个年级成绩好些)。
(3)如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强些?并说明理由。
解:(1)
|
年级 |
平均数 |
众数 |
中位数 |
|
初一年级 |
85.5 |
80 |
87 |
|
初二年级 |
85.5 |
85 |
86 |
|
初三年级 |
85.5 |
78 |
84 |
(2)①∵平均数都相同,初二年级的众数最高,∴初二年级的成绩好一些;
②∵平均数都相同,初一年级的中位数最高,∴初一年级的成绩好一些。
(3)∵初一、初二、初三各年级前三名学生决赛成绩的平均分分别是93分、91分、94分,∴从各年级参加决赛的选手中分别选出3人参加总决赛,初三年级的实力更强一些。
例11、(2004 河北)光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台。先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区。 两地区与该农机租赁公司商定的每天的租赁价格见下表:
|
|
每台甲型收割机的租金 |
每台乙形收割机的租金 |
|
A地区 |
1800元 |
1600元 |
|
B地区 |
1600元 |
1200元 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议。
解:(1)若派往A地区的乙型收割机为x台,则派往A地区的甲型收割机为(30-x)台;派往B地区的乙型收割机为(30-x)台,派往B地区的甲型收割机为(x-10)台。
∴y=1600x+1800(30-x)+1200(30-x)+1600(x-10)=200x+74000
x的取值范围是:10≤x≤30(x是正整数)
(2)由题意得 200x+74000≥79600
解不等式得 x≥28 由于10≤x≤30(x是正整数)
∴x取28,29,30这三个值。
∴有3种不同的分配方案。
①当x=28时,即派往A地区的甲型收割机为2台,乙型收割机为28台;派往B地区的甲型收割机为18台,乙型收割机为2台。
②当x=29时,即派往A地区的甲型收割机为1台,乙型收割机为29台;派往B地区的甲型收割机为19台,乙型收割机为1台。
③当x=30时,即30台乙型收割机全部派往A地区;20台甲型收割机全部派往B地区。
(3)由于一次函数y=200x+74000的值y是随着x的增大而增大的,所以当x=30时,y取得最大值。如果要使农机租赁公司这50台联合收割机每天获得租金最高,只需x=30,此时,y=6000+74000=80000。
建议农机租赁公司将30台乙型收割机全部派往A地区;20台甲型收割机全部派往B地区,可使公司获得的租金最高。
例12、(2004 芜湖)某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5米3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:
① 求出y与x的函数关系式.(纯利润=总收入-总支出)
② 当y=106000时,求该厂在这个月中生产产品的件数.
解:①依题意得:y=80x-60x-0.5x·2-8000
y=19x-8000
∴所求的函数关系式为y=19x-8000(x>0且x是整数)
②当y=106000时,代入得:
106000=19x-8000
19x=114000
x=6000
∴这个月该厂生产产品6000件.
例13(2004 四川)某零件制造车间有工人20名,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利润150元,每制造一个乙种零件可获利润260元,在这20名工人中,车间每天安排x名工人制造甲种零件,其余工人制造乙种零件.
(I)请写出此车间每天所获利润y(元)与x(人)之间的函数关系式;
(II)若要使车间每天所获利润不底于24,000元,你认为至少要派多少名工人去制造乙种零件才合适?
解:(1)依题意,是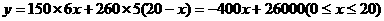
(2)由题意:有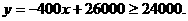
解得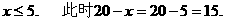
答:至少要派15名工人去制造乙种零件才合适.
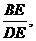 ∴BE=DE·tan∠BDE=
∴BE=DE·tan∠BDE=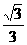 DE.
DE.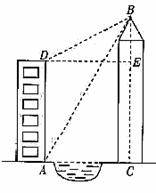 在Rt△BAC中,∵tan∠BAC=
在Rt△BAC中,∵tan∠BAC=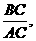
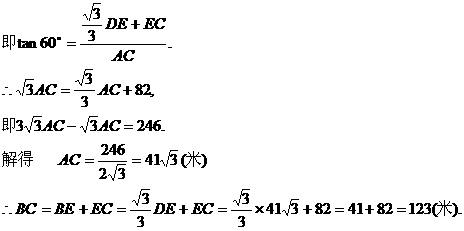
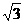 米
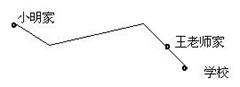
米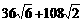 )千米的海面上,目前台风中心正以20千米/时的速度向北偏西60°的方向移动,距台风中心50千米的圆形区域均会受到强袭击.已知宁海位于宁波正南方向72千米处,象山位于宁海北偏东60°方向56千米处.请问:宁波、宁海、象山是否会受这次台风的强袭击?如果会,请求出受强袭击的时间;如果不会,请说明理由.(为解决问题,须画出示意图,现已画出其中一部分,请根据需要,把图形画完整)
)千米的海面上,目前台风中心正以20千米/时的速度向北偏西60°的方向移动,距台风中心50千米的圆形区域均会受到强袭击.已知宁海位于宁波正南方向72千米处,象山位于宁海北偏东60°方向56千米处.请问:宁波、宁海、象山是否会受这次台风的强袭击?如果会,请求出受强袭击的时间;如果不会,请说明理由.(为解决问题,须画出示意图,现已画出其中一部分,请根据需要,把图形画完整)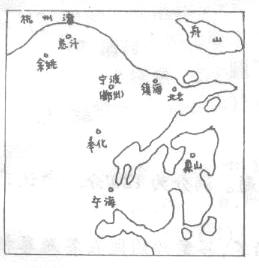
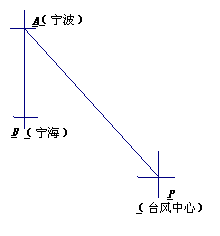
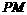 经过点
经过点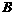 .
.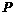 作东西方向(水平)直线与
作东西方向(水平)直线与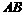 (南北)延长线交于
(南北)延长线交于 ,
,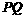 与
与 相交于
相交于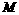 .
.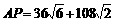 ,
,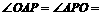 45°,
45°,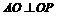 ,
,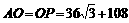 ,
,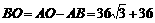 .
.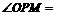 30°,
30°,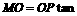 30°=
30°=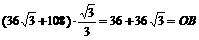 ,
,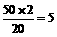 (时) .
(时) . 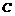 为象山,由题意可得
为象山,由题意可得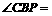 30°+30°=60°,
30°+30°=60°,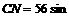 60°=
60°=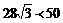 ,
, 为半径的圆与
为半径的圆与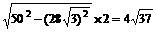 ,
,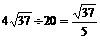 (时)
(时)  到
到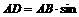 60°=
60°=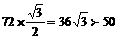 ,
,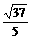 时.(约1时13分)
时.(约1时13分)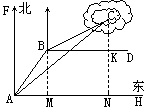 的危险?
的危险?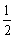 AB=5,BM=5
AB=5,BM=5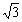 .
. 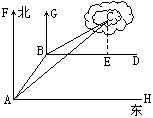 解法二:过点C作CE⊥BD,垂足为E,∴CE∥GB∥FA.
解法二:过点C作CE⊥BD,垂足为E,∴CE∥GB∥FA.


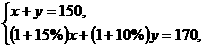
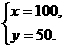
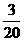 ,公司第二次再改装同样多的车辆后,所有改装后的车辆每天的燃料费占剩下末改装车辆每天燃料费用的
,公司第二次再改装同样多的车辆后,所有改装后的车辆每天的燃料费占剩下末改装车辆每天燃料费用的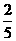 。问:
。问: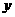 辆车,改装后的每辆出租车每天的燃料费比改装前的燃料费下降的百分数为
辆车,改装后的每辆出租车每天的燃料费比改装前的燃料费下降的百分数为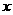
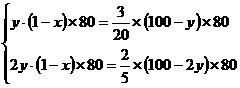
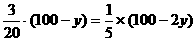
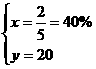
 天可以收回成本,则:
天可以收回成本,则: 根据题意,得:
根据题意,得:
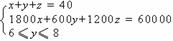
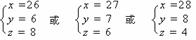 …………
………… 
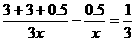 20分钟=
20分钟=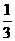 小时
小时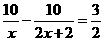 .
. 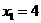 ,
,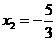 .
.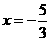 不合题意,舍去.
不合题意,舍去. 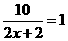 (小时),
(小时),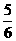 小时.
小时.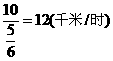 ,12-10=2(千米/时).
,12-10=2(千米/时).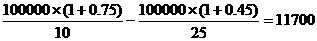 (万元)
(万元)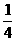 ,需要在这个口袋中再放入多少个绿球?
,需要在这个口袋中再放入多少个绿球? (3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.