16.我市东辛农场A、B两个分场得知得知南京和上海两个城市急需粮食240吨和260吨的消息后,决定向两个城市调运粮食。已知A分场有粮食200吨,B分场有粮食300吨,现将这些粮食全部调往两个城市。从A分场运往两城市的费用分别为每吨20元和25元,从B分场运往两个城市的费用分别为每吨15元和18元。设从B分场运往南京的粮食为x吨。
(1)请填写下表,并求两个粮食分场调运粮食的运费相等时的x的值;
|
|
南京 |
上海 |
总计 |
|
A |
|
|
200吨 |
|
B |
x吨 |
|
300吨 |
|
总计 |
240吨 |
260吨 |
500吨 |
(2)设A、B两个分场的总运费为w元,写出w与x之间的函数关系式,并求总运费最小的调运方案;
[试题来源]改编自2008年中考题.
[命题意图]①本题综合考查了一次方程、一次函数和一次不等式在实际问题中的应用,考查了学生对于基础知识的应用与创新能力.
②随着新课程改革的逐步展开与深入,涉及三个“一次”的内容应体现对学生基础知识、基本能力的考查.
③师向学生讲明白:一般情况下,在自变量的取值范围内,自变量有几个值,就有几种设计方案.
[参考答案](1)
|
|
南京 |
上海 |
总计 |
|
A |
(240-x)吨 |
(x-40)吨 |
200吨 |
|
B |
x吨 |
(300-x)吨 |
300吨 |
|
总计 |
240吨 |
260吨 |
500吨 |
依题意得: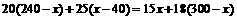 .
.
解得: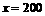 .
.
(2) w与x之间的函数关系为: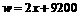 .
.
依题意得: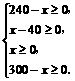 . ∴40≤
. ∴40≤ ≤240
≤240
在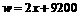 中,∵2>0, ∴
中,∵2>0, ∴ 随
随 的增大而增大,
的增大而增大,
|
|
南京 |
上海 |
|
A |
200吨 |
0吨 |
|
B |
40吨 |
260吨 |
故当 =40时,总运费最小,
=40时,总运费最小,
此时调运方案为如右表。
15.为了参加数学竞赛,八年级(3)班准备从甲、乙、丙三位男同学和A、B两位女同学中选取一位男同学和一位女同学参赛.
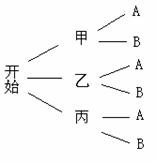
(1)若随机选一位男同学和一位女同学,用树状图(或列表法)表示所有可能出现的结果;
(2)求恰好选中男同学甲和女同学A的概率.
[试题来源]原创
[命题意图]①考核学生对随机现象与概率意义的理解、对现实生活中随机现象的分析能力.
②列表或画树状图进行比较分析,找出所有等可能结果,利用概率进行说明.
③解答本题的关键是准确地列举所有可能得到的男同学和女同学的组合.
[参考答案](1)①列表法: ②树状图:
  |
A |
B |
|
甲 |
(甲,A) |
(甲,B) |
|
乙 |
(乙,A) |
(乙,B) |
|
丙 |
(丙,A) |
(丙,B) |

 (2)
(2)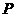 (恰好选中男同学甲和女同学A)=
(恰好选中男同学甲和女同学A)=
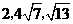 已知直角三角形的两边求第三边或利用勾股定理得到有关线段之间的关系是中考内容的重中之重,出现频率较高,一般以选择题、填空题或计算题的形式出现,有时也作为一道综合题的一个考查点出现。近似数、有效数字知识常与科学记数法、无理数一起出现在中考试题中,为必考内容。
已知直角三角形的两边求第三边或利用勾股定理得到有关线段之间的关系是中考内容的重中之重,出现频率较高,一般以选择题、填空题或计算题的形式出现,有时也作为一道综合题的一个考查点出现。近似数、有效数字知识常与科学记数法、无理数一起出现在中考试题中,为必考内容。
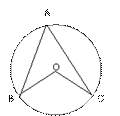
 (2007青岛)如图所示圆柱的左视图是( ).
(2007青岛)如图所示圆柱的左视图是( ).

 (2005武汉)一次函数y=x+1的图象在( ).
(2005武汉)一次函数y=x+1的图象在( ). 下列图形中,不是轴对称图形的是( )
下列图形中,不是轴对称图形的是( )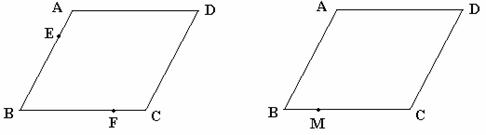
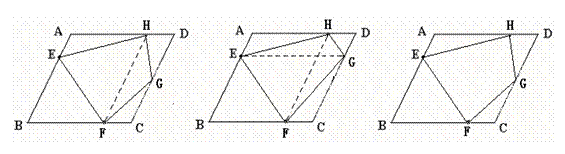
 方案(2)
方案(2)
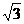 ,0)时,求此时DP的长及点D的坐标;
,0)时,求此时DP的长及点D的坐标;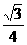 ,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
,若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

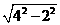 =
=

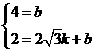
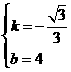 )
)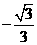 x+4
x+4
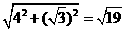 .
. 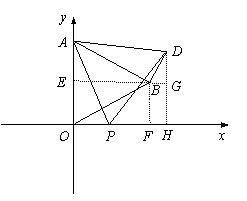 在Rt△BDG中,∠BGD=900,
∠DBG=600.
在Rt△BDG中,∠BGD=900,
∠DBG=600.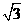 ×
× =
=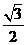 .
.
 .
.  , DH=
, DH=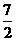
 而AE=2, BD=OP=
而AE=2, BD=OP=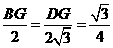 ,解得BG=
,解得BG= .
.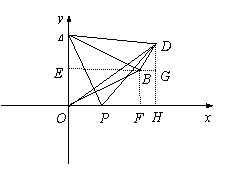 设点P为(t,0),下面分三种情况讨论:
设点P为(t,0),下面分三种情况讨论: ,
, 解得
解得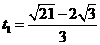 ,
, 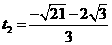 ( 舍去) .
( 舍去) . 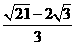 ,
0 )
,
0 ) <t≤0时,如图,
<t≤0时,如图,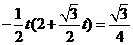 ,
,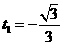 ,
, 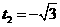 .
.
 ∴点P2的坐标为(
∴点P2的坐标为(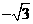 ,
0).
,
0).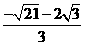 ,
0)
,
0)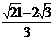 ,
0)、P2 (
,
0)、P2 (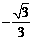 ,
0)、P3 (
,
0)、P3 (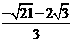 , 0)。
, 0)。