14.雪岩在八年级下学期的数学成绩如下表所示
|
测
试类别 |
平 时 |
期 中考 试 |
期 末 考 试 |
|||
|
测验1 |
测验2 |
测验3 |
课 题学 习 |
|||
|
成绩 |
88 |
70 |
98 |
86 |
90 |
87 |

(1) 计算该学期的平时平均成绩.
(2) 如果学期的总评成绩是根据扇形统计图所示的权重计算,请计算出雪岩在 该学期的总评成绩.
[试题来源]改编自2008年中考题.
[命题意图]①考察学生算术平均数与加权平均数的应用能力.
②以扇形统计图形式展示权重,既考核了平均数知识又体现识别统计图能力.
③解决有关统计图的问题关键在于“读图”,理解图象中所蕴含的信息.
[参考答案](1)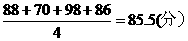
(2)85.5×10%+90×30%+87×60%=87.75(分)
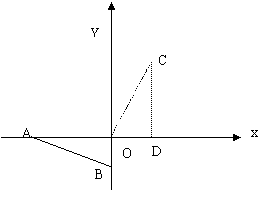
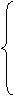 4a-2b+c=0
解得a=
4a-2b+c=0
解得a=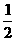 ,b=
,b=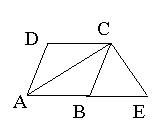 13.如图,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC且与AB的延长线交与点E.求证:四边形AECD是等腰梯形.
13.如图,在菱形ABCD中,∠DAB=60°,过点C作CE⊥AC且与AB的延长线交与点E.求证:四边形AECD是等腰梯形.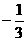 )-2+(-1)2009
)-2+(-1)2009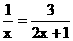
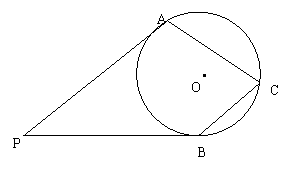 11.如图,PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,若∠APB=40°,求∠ACB的度数.
11.如图,PA、PB是⊙O的切线,切点分别为A、B,C是⊙O上一点,若∠APB=40°,求∠ACB的度数.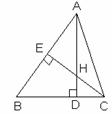 [命题意图]①考核学生对三角形全等判定方法的掌握情况.
[命题意图]①考核学生对三角形全等判定方法的掌握情况.
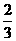
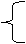 3x-6<4-x
3x-6<4-x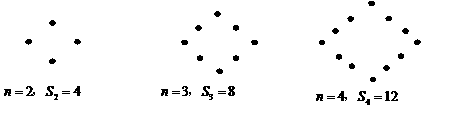

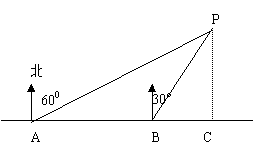 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°的方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°的方向上,则灯塔P到环海路的距离PC= 米(用根号表示).
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在北偏东60°的方向上,在A处东500米的B处,测得海中灯塔P在北偏东30°的方向上,则灯塔P到环海路的距离PC= 米(用根号表示).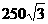
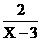 有意义,则X应满足的条件是( )
有意义,则X应满足的条件是( )