23.(本小题满分12分)
由于电力紧张,某地决定对工厂实行鼓励错峰用电.规定:在每天的7:00至24:00为用电高峰期,电价为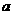 元/度;每天0:00至7:00为用电平稳期,电价为
元/度;每天0:00至7:00为用电平稳期,电价为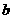 元/度.下表为某厂4、5月份的用电量和电费的情况统计表:
元/度.下表为某厂4、5月份的用电量和电费的情况统计表:
|
月份 |
用电量(万度) |
电费(万元) |
|
4 |
12 |
6.4 |
|
5 |
16 |
8.8 |
(1)若4月份在平稳期的用电量占当月用电量的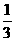 ,5月份在平稳期的用电量占当月用电量的
,5月份在平稳期的用电量占当月用电量的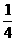 ,求
,求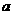 、
、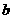 的值.
的值.
(2)若6月份该厂预计用电20万度,为将电费控制在10万元至10.6万元之间(不含10万元和10.6万元),那么该厂6月份在平稳期的用电量占当月用电量的比例应在什么范围?
[命题意图]本题是一道与生活联系紧密的应用题,考查列二元一次方程组、一元一次不等式解决问题能力,渗透数学模型化思想方法。
[参考答案](1) 由题意,得
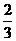 ×12a+
×12a+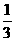 ×12b=6.4
×12b=6.4
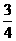 ×16a+
×16a+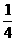 ×16b=8.8
×16b=8.8
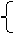 8a+4b=6.4
8a+4b=6.4
12a+4b=8.8
解得 a=0.6 b=0.4
(2) 设6月份在平稳期的用电量占当月用电量的比例为k.
由题意,得10<20(1-k)×0.6+20k×0.4<10.6
解得 0.35<k<0.5
答:该厂6月份在平稳期的用电量占当月用电量的比例在35%到50%之间(不含35%和50%).
[试题来源]重庆05中考题
24.(7分)小明和小颖做掷骰子的游戏,规则如下:
①游戏前,每人选一个数字;
②每次同时掷两枚均匀骰子;
③如果同时掷得的两枚骰子点数之和,与谁所选数字相同,那么谁就获胜.
(1)不全下表,列出同时掷两枚均匀骰子所有可能出现的结果:
 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
|
|
(1,3) |
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
(2)小明选的数字是9,小颖选的数字是6.如果你也加入游戏,你会选什么数字,使自己获胜的概率比他们大?请说明理由.
[命题意图]本题以掷骰子的游戏为背景,考查了求概率的基本技能--列表法,还渗透了计算说理。
[参考答案]
 (1)填表正确;··········································································································· 4分
(1)填表正确;··········································································································· 4分
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
(1,5) |
(1,6) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
(2,5) |
(2,6) |
|
3 |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
(3,5) |
(3,6) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
(4,5) |
(4,6) |
|
5 |
(5,1) |
(5,2) |
(5,3) |
(5,4) |
(5,5) |
(5,6) |
|
6 |
(6,1) |
(6,2) |
(6,3) |
(6,4) |
(6,5) |
(6,6) |
(2)由上表可看出,同时投掷两枚骰子,可能出现的结果有36种,它们出现的可能性相同.
所有的结果中,满足两枚骰子点数和为9(记为事件 )的结果有4种,即(3,6),(4,5),(5,4),(6,3),所以小明获胜的概率为
)的结果有4种,即(3,6),(4,5),(5,4),(6,3),所以小明获胜的概率为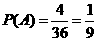 ;························ 6分
;························ 6分
满足两枚骰子点数和为6(记为事件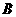 )的结果有5种,即(1,5),(2,4),(3,3)(4,2),(5,1),所以小颖获胜的概率为
)的结果有5种,即(1,5),(2,4),(3,3)(4,2),(5,1),所以小颖获胜的概率为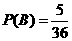 ;······························ 8分
;······························ 8分
要想使自己获胜的概率比他们大,必须满足两枚骰子点数和出现的结果多于5种,由所列表格可知,只有两枚骰子点数和为7(记为事件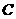 )的结果多于5种,有6种,即(1,6),(2,5),(3,4)(4,3),(5,2),(6,1),所以
)的结果多于5种,有6种,即(1,6),(2,5),(3,4)(4,3),(5,2),(6,1),所以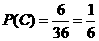 .因此,要想使自己获胜的概率比他们大,所选数字应为7.············· 12分
.因此,要想使自己获胜的概率比他们大,所选数字应为7.············· 12分
[试题来源]改编自2008年南京中考数学试题
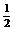 C.
C.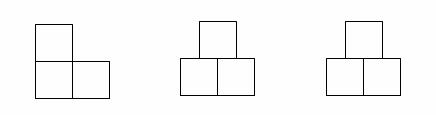
 解:(1)
解:(1)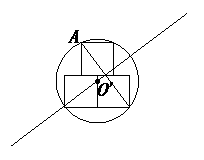 (2)方法一:
方法二:
(2)方法一:
方法二: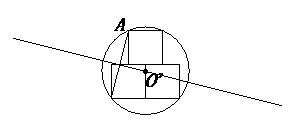
 为所求作的圆.
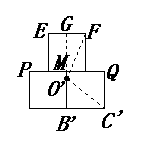
为所求作的圆. 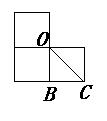 (3)辅助线如图,设
(3)辅助线如图,设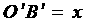 ,
,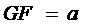 ,
,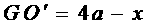 ,又
,又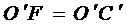
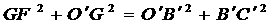 ,
, 即
即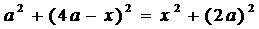
 ,
,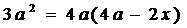 ,
,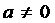 ∴
∴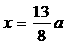 ,
,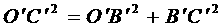 =
=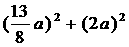 =
=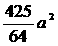
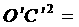
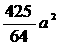 <
<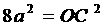 ,∴
,∴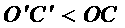 ,
, 3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.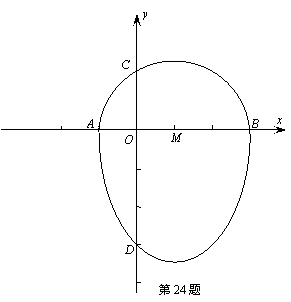
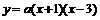 (a≠0)
(a≠0) 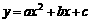 (a≠0)
(a≠0)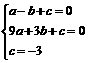 ,解之得:
,解之得: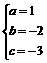
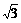
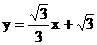 ······················· 8分
······················· 8分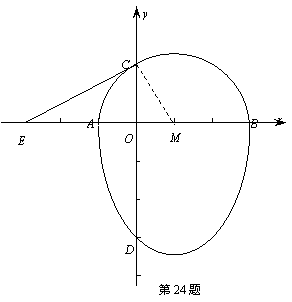 (3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0) ············ 9分
(3)设过点D(0,-3),“蛋圆”切线的解析式为:y=kx-3(k≠0) ············ 9分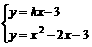 只有一组解
只有一组解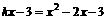 有两个相等实根,∴k=-2····· 11分
有两个相等实根,∴k=-2····· 11分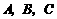 三种型号,它们的数量比例以及每人每小时组装各种型号学具的数量如图所示:
三种型号,它们的数量比例以及每人每小时组装各种型号学具的数量如图所示: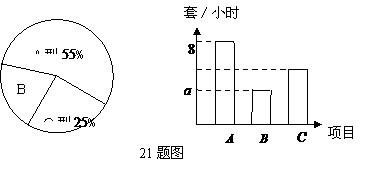

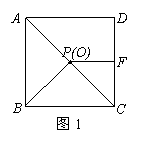

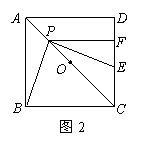

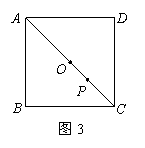

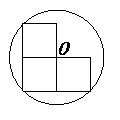
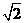 CE;
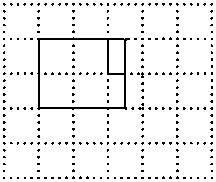
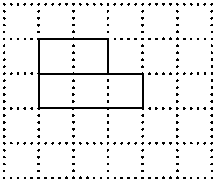
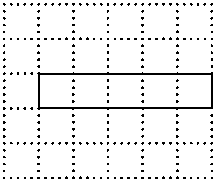
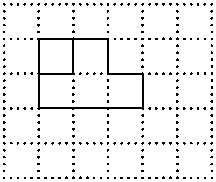
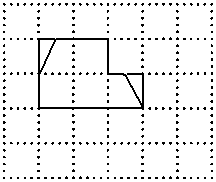
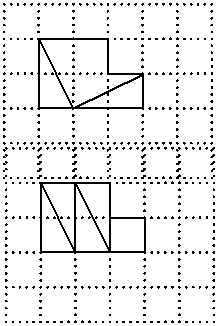
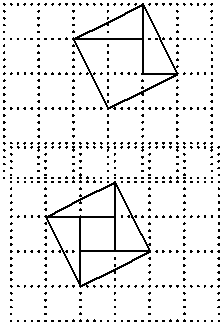
CE;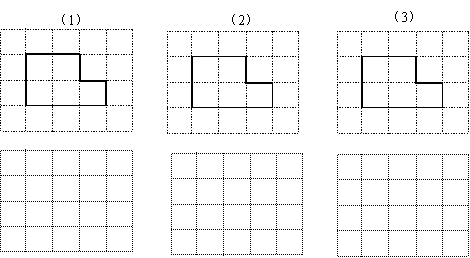 请在方格纸中的图形上画出分割线,在相应的下边的方格纸上面拼接后的图形。
请在方格纸中的图形上画出分割线,在相应的下边的方格纸上面拼接后的图形。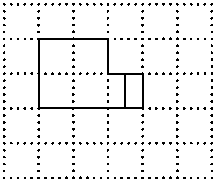


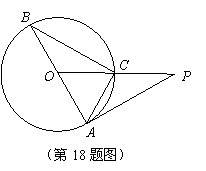 如图,
如图, 内接于⊙O,
内接于⊙O, 为⊙O的直径,
为⊙O的直径,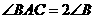 ,
,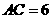 ,过点
,过点 的延长线交于点
的延长线交于点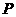 ,求
,求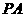 的长.
的长.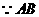 是⊙O的直径,
是⊙O的直径,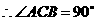 .又
.又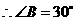 ,
,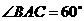 .························ 3分
.························ 3分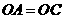 ,所以
,所以 是等边三角形,由
是等边三角形,由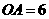 .······· 5分
.······· 5分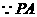 是⊙O的切线,
是⊙O的切线,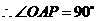 .
. 中,
中,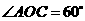 ,
,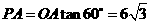 . ······················ 8分
. ······················ 8分