摘要:13.如图.在梯形中..过对角线的中点作.分别交边于点.连接. (1)求证:四边形是菱形, (2)若.. 求四边形的面积. (1)证明:方法1:.. 在和中. .. 又.四边形是平行四边形. .四边形是菱形. 方法2:证同方法1. ..四边形是平行四边形. . 是的垂直平分线.. 四边形是菱形. (2)解:四边形是菱形.. . 在中... . . 核心精神---创新关
网址:http://m.1010jiajiao.com/timu3_id_456614[举报]
如图,在梯形ABCD中,AB∥DC,过对角线AC的中点O作EF⊥AC,分别交边AB、CD于点E、F,连接 CE、AF.
CE、AF.
(1)求证:四边形AECF是菱形;
(2)若EF=4,tan∠OAE=
,求四边形AECF的面积.
查看习题详情和答案>>
 CE、AF.
CE、AF.(1)求证:四边形AECF是菱形;
(2)若EF=4,tan∠OAE=
| 2 | 5 |
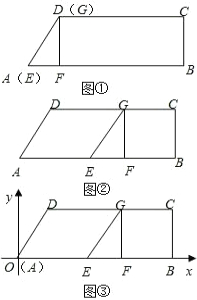 如图①,在梯形ABCD中,CD∥AB,∠ABC=90°,∠DAB=60°,AD=2,CD=4.另有一直角三角形EFG,∠EFG=90°,点G与点D重合,点E与点A重合,点F在AB上,让△EFG的边EF在AB上,点G在DC上,以每秒1个单位的速度沿着AB方向向右运动,如图②,点F与点B重合时停止运动,设运动时间为t秒.
如图①,在梯形ABCD中,CD∥AB,∠ABC=90°,∠DAB=60°,AD=2,CD=4.另有一直角三角形EFG,∠EFG=90°,点G与点D重合,点E与点A重合,点F在AB上,让△EFG的边EF在AB上,点G在DC上,以每秒1个单位的速度沿着AB方向向右运动,如图②,点F与点B重合时停止运动,设运动时间为t秒.(1)在上述运动过程中,请分别写出当四边形FBCG为正方形和四边形AEGD为平行四边形时对应时刻t的值或范围;
(2)以点A为原点,以AB所在直线为x轴,过点A垂直于AB的直线为y轴,建立如图③所示的坐标系.求过A,D,C三点的抛物线的解析式;
(3)探究:延长EG交(2)中的抛物线于点Q,是否存在这样的时刻t使得△ABQ的面积与梯形ABCD的面积相等?若存在,求出t的值;若不存在,请说明理由. 查看习题详情和答案>>
 中,
中, ∥
∥ ,过对角线
,过对角线 的中点
的中点 作
作 ,分别交边
,分别交边 于点
于点 ,连接
,连接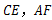 .
.
 是菱形;
是菱形; ,
, ,求四边形
,求四边形 的面积.
的面积.
