0 44923 44931 44937 44941 44947 44949 44953 44959 44961 44967 44973 44977 44979 44983 44989 44991 44997 45001 45003 45007 45009 45013 45015 45017 45018 45019 45021 45022 45023 45025 45027 45031 45033 45037 45039 45043 45049 45051 45057 45061 45063 45067 45073 45079 45081 45087 45091 45093 45099 45103 45109 45117 447348
 ;
;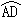 =
= 以及
以及 ∽
∽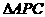 ∽
∽ 等结论,由此可得,切线长定理是证明线段相等、角相等、弧相等、线段成比例,垂直关系的重要依据。
等结论,由此可得,切线长定理是证明线段相等、角相等、弧相等、线段成比例,垂直关系的重要依据。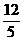 ,大于
,大于 ,90,相切;
,90,相切;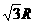 ; (6)
; (6)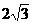 ; (7)115
; (7)115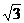 ,1,
,1, 。
。 ,点O到直线I的距离为
,点O到直线I的距离为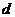 ,若⊙O与
,若⊙O与 至多只有一个公共点,则
至多只有一个公共点,则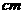 ,若以A为圆心,2
,若以A为圆心,2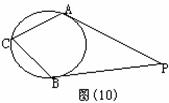
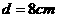 时,直线与圆
;当
时,直线与圆
;当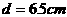 时,直线与圆 。
时,直线与圆 。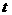 △ABC中,∠C=90O,AC=3
△ABC中,∠C=90O,AC=3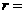
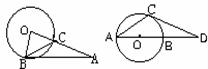 图(8)
图(8)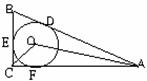
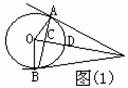
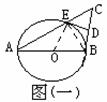 AB是⊙O的直径,CB⊥AB,AC交⊙O于E,D是的BC的中点,
AB是⊙O的直径,CB⊥AB,AC交⊙O于E,D是的BC的中点,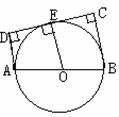 图(2)
图(2) 图(3)
图(3) ED平分∠ADC
ED平分∠ADC
 DA⊥EA于A ÞEA=EF E为AB中点
DA⊥EA于A ÞEA=EF E为AB中点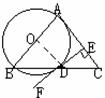 图(4)
图(4)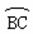 于D,过D的切线分别交AB、AC的延长线于E、F,
于D,过D的切线分别交AB、AC的延长线于E、F,
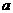 ,
,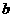 ,
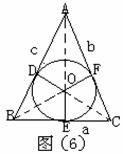
,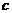 ,面积为S,内切圆⊙O的半径为
,面积为S,内切圆⊙O的半径为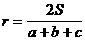
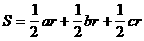 。
。
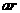 S△AOC=
S△AOC=
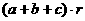
 。
。