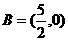0 44943 44951 44957 44961 44967 44969 44973 44979 44981 44987 44993 44997 44999 45003 45009 45011 45017 45021 45023 45027 45029 45033 45035 45037 45038 45039 45041 45042 45043 45045 45047 45051 45053 45057 45059 45063 45069 45071 45077 45081 45083 45087 45093 45099 45101 45107 45111 45113 45119 45123 45129 45137 447348
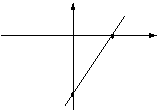
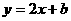 的图象与坐标轴围成的三角形的面积是9,则
的图象与坐标轴围成的三角形的面积是9,则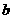 =____.
=____.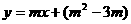 图象过原点,则
图象过原点,则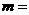 ____.若图象与
____.若图象与 轴交于点(0,4),则
轴交于点(0,4),则 =____.
=____. 的图象经过点(-2,6),则它的图象经过第____象限,它的图象 象与
的图象经过点(-2,6),则它的图象经过第____象限,它的图象 象与 交于____,与
交于____,与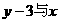 成正比例,且
成正比例,且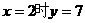
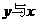 间的函数解析式.
间的函数解析式.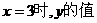 .
.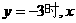 的值.
的值.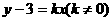
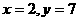 代入上式得k=2
代入上式得k=2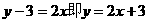
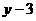 看成一个变量
看成一个变量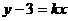 .
.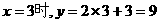 .
.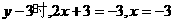 .
.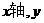 轴的交点坐标及它的图象与两坐标轴围成的三角形面积.
轴的交点坐标及它的图象与两坐标轴围成的三角形面积.
 将
将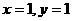 和
和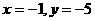 代入得
代入得 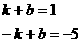
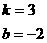
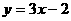
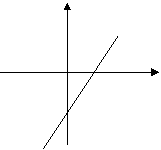 (2)对
(2)对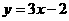 ,令
,令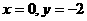 则图象与
则图象与 A(0,-2)令
A(0,-2)令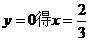 ,则此函数与
,则此函数与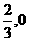 ).
y
).
y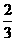 |个单位,高|-2|=2
A(0,-2)
|个单位,高|-2|=2
A(0,-2) 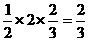
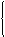 设另一条直线为y1=k1x+b,将x=-1,y=-5.x=0,y=4代入得
设另一条直线为y1=k1x+b,将x=-1,y=-5.x=0,y=4代入得 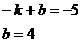

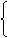 ∴
∴ 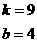
 ∴C在y=2x-3上
∴C在y=2x-3上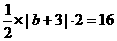 y=kx+b
y=kx+b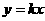 ,求一次函数的解析式时,先设
,求一次函数的解析式时,先设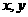 的值就可以,因为它只有一个待定系数;而求一次函数
的值就可以,因为它只有一个待定系数;而求一次函数 两条直线
两条直线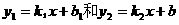 的交点坐标是方程组
的交点坐标是方程组 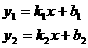 的解.如y=x-2和y=-3x+1的交点坐标就是方程组
的解.如y=x-2和y=-3x+1的交点坐标就是方程组 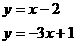 的解
的解 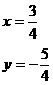 即交点坐标是(
即交点坐标是(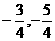 )。
)。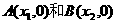 ,则A、B两点的距离是| x2-x1|,如(-1,0)和(3,0)两点的距离就是|3-(-1)|=4,在
,则A、B两点的距离是| x2-x1|,如(-1,0)和(3,0)两点的距离就是|3-(-1)|=4,在
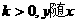 的增大而增大,
的增大而增大,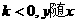 的增大而减少,此性质反映在图象上是
的增大而减少,此性质反映在图象上是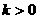 时图象自左而右是“上升”的,如
时图象自左而右是“上升”的,如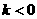 图象自左而右是“下降”的,如
图象自左而右是“下降”的,如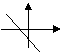
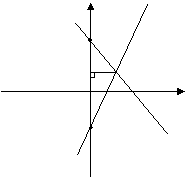
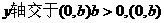 在
在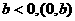 在
在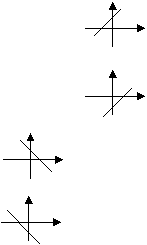 y
y 的图象在一、二、三象限 0 x
的图象在一、二、三象限 0 x 的图象在一、三、四象限 0 x
的图象在一、三、四象限 0 x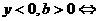 图象在一、二、四象限 0 x
图象在一、二、四象限 0 x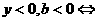 图象在二、三、四象限 0 x
图象在二、三、四象限 0 x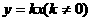 和一次函数
和一次函数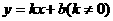 的图象都是一条直线,既然是一条直线,我们只要描出两点即可确定该直线。因为正比例函数是过原点的直线,当然坐标原点是所描的两点中的一个,另外一个是
的图象都是一条直线,既然是一条直线,我们只要描出两点即可确定该直线。因为正比例函数是过原点的直线,当然坐标原点是所描的两点中的一个,另外一个是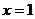 时y=k就是点
时y=k就是点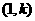 ,所以正比例函数的图像是过(0,0)、(1,k)两点的直线。而一次函数与两条坐标轴各有一个交点(注意:与x轴、y轴交点的坐标是极其重要的),那么“两点确定一条直线”中的两点就可以取这两个交点,由于一次函数与x轴的交点必在x轴上,而在x轴上的点的特点是纵坐标为0,即:在一次函数
,所以正比例函数的图像是过(0,0)、(1,k)两点的直线。而一次函数与两条坐标轴各有一个交点(注意:与x轴、y轴交点的坐标是极其重要的),那么“两点确定一条直线”中的两点就可以取这两个交点,由于一次函数与x轴的交点必在x轴上,而在x轴上的点的特点是纵坐标为0,即:在一次函数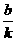 ,从而得出一次函数
,从而得出一次函数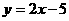 的图象:令
的图象:令 ,令
,令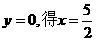 ,所以
,所以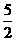 ,0)两点的直线。
,0)两点的直线。