摘要:例1. 已知:如图(1)AB是⊙O的直径.CB⊥AB.AC交⊙O于E.D是的BC的中点. 求证:直线DE是⊙O的切线. 证明:连结OE.BE. ∵AB是⊙O的直径.∴∠AEB=90O. ∴BE⊥AC.则∠BEC=90O. 又∵D是BC的中点. ∴DE=BD=BC.∴∠DBE=∠DEB ∵OE=OB ∴∠OBE=∠OEB 因此:∠DBE+∠OBE=∠DEB+∠OEB 即:∠OED=∠OBD ∵BC⊥AB 即:∠OBD=90O ∴∠OED=90O 则DE是⊙O的切线. 评析:(1) 此例是由直径.圆周角.直角三角形斜边上的中线.切线的判定等知识构成的命题.(2) 证一条直线是圆的切线,常用的两个判定方法是:直线过圆上一已知点时.作过这点的半径转证直线垂直于这条半径,直线和圆的公共点的位置未知时.过圆心作到直线的距离.转证此距离等于圆的半径.此例显然用的是第一种方法.(3)此题的分析思路:要证DE是圆的切线.而E在圆上.据圆的切线的定义则E是切点.所以应连结OE.转证DE⊥OE. 例2. 已知:如图(2)所示.在直角梯形ABCD中.AD⊥CD于D.BC⊥CD于D.且AD+CB=AB.以斜腰AB为直径作⊙O. 求证:CD是⊙O的切线. 图(2) 分析:要证CD是⊙O的切线.切点在什么位置呢?无法判定.因此应该用证明切线的第二种方法.作圆心到直线的距离OE.转而证OE等于圆的半径. 证明:过O作OE⊥CD于E. ∵AD⊥CD.BC⊥CD ∴AD||OE||BC ∵O是AB中点.则E是CD中点. ∴OE是梯形ABCD的中位线. ∴OE= 又∵AD+BC=AB ∴OE=AB. 则DC是⊙O的切线. 例3. 如图(3)所示.在直角梯形ABCD中.∠A=∠B=90O.E为AB上的一点.ED平分∠ADC.EC平分∠BCD. 求证:以AB为直径的圆与DC相切.图(3) 分析:要证以AB为直径的圆与DC相切.只需证AB的中点到DC的距离等于AB. 证明:过点E作EF⊥CD于F. ED平分∠ADC DA⊥EA于A ÞEA=EF E为AB中点 EF⊥DF于F Þ 同理可证:EF=EB EF=AB Þ以AB为直径的圆与CD相切. 例4. 如图(3)所示.已知△ABC中.以AB为直径作⊙O交BC于D.过D作⊙O的切线FE.交AC于E.且AE⊥DE. 求证:AB=AC 图(4) 证明:连结OD ∵DE切⊙O于D.则OD⊥DE ∵AE⊥DE. ∴OD∥AC 则∠C=∠ODB ∵OB=OD ∴∠B=∠ODC ∴∠B=∠C 则AB=AC 例5. 已知:如图(5)所示.△ABC是⊙O的内接三角形.∠BAC的平分线交于D.过D的切线分别交AB.AC的延长线于E.F. 求证:BC||EF 证明:连结OD ∵EF切⊙O于D. ∴EF⊥OD ∵AD平分∠BAC ∴∠BAD=∠CAD 则 由垂径定理.知:OD⊥BC ∴BC∥EF 注:此证法运用切线的性质比较灵活巧妙.只要在已知切线时用垂直方法的意识强.则不难想到. 例6. 如图(6)所示.△ABC三边长为...面积为S.内切圆⊙O的半径为.⊙O与△ABC的三边相切于D.E.F. 求证: 分析:要证.只需证:. 证明:连结OA.OB.OC ∵⊙O切△ABC的三边于D.E.F ∴OD⊥AB.OE⊥BC.OF⊥AC ∴S△AOB=OD·AB= 同理可得:S△BOC= S△AOC= ∴S=S△AOB+S△BOC+S△AOC= ∴ 注:若∠C=90O.则有:.
网址:http://m.1010jiajiao.com/timu3_id_450201[举报]
22、已知:如图1,从以AB为直径的圆上一点D引一切线,再从AB上一点C引这条切线的垂线,垂足为E.
(1)如果DC⊥AB且DC交圆于点F,请证明:CE•AB=AC•CB+CD2;


(2)如果DC与AB不垂直如图2,那(1)中结论是否还成立?请证明你的想法.
查看习题详情和答案>>
(1)如果DC⊥AB且DC交圆于点F,请证明:CE•AB=AC•CB+CD2;


(2)如果DC与AB不垂直如图2,那(1)中结论是否还成立?请证明你的想法.
已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长 线于点E.
线于点E.
(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积. 查看习题详情和答案>>
 线于点E.
线于点E.(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=6,求△ACD的面积. 查看习题详情和答案>>
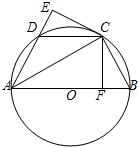 29、已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.求证:DE=BF.
29、已知:如图,AB是⊙O的直径,点C、D为圆上两点,且弧CB=弧CD,CF⊥AB于点F,CE⊥AD的延长线于点E.求证:DE=BF.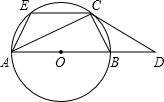
 已知:如图,AB是⊙O的直径,弦AD∥OC.求证:
已知:如图,AB是⊙O的直径,弦AD∥OC.求证: