0 44904 44912 44918 44922 44928 44930 44934 44940 44942 44948 44954 44958 44960 44964 44970 44972 44978 44982 44984 44988 44990 44994 44996 44998 44999 45000 45002 45003 45004 45006 45008 45012 45014 45018 45020 45024 45030 45032 45038 45042 45044 45048 45054 45060 45062 45068 45072 45074 45080 45084 45090 45098 447348
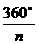 .
.
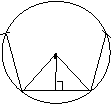
 )
) 边形
边形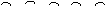 ②经过各分点做圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正
②经过各分点做圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正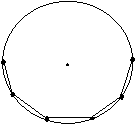 且AB=BC=CD=DE=…….
且AB=BC=CD=DE=…….  ∴ AB=BC=CD=DE……
∴ AB=BC=CD=DE…… 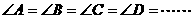
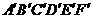 ……是圆外切n边形,切点分别是A,B,C,D,E……,
……是圆外切n边形,切点分别是A,B,C,D,E……,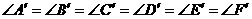 =…….
=……. 和四边形BOC
和四边形BOC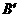 中
中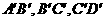 切⊙O于B,C,D
切⊙O于B,C,D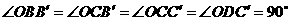








 ∴
∴ 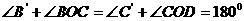 A
F
A
F 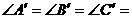 ……
……

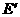
 ∴
∴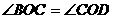
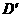

 D
D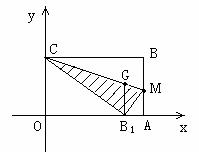 (1)如图,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作B1点,求B1点的坐标;
(1)如图,在AB上取一点M,使得△CBM沿CM翻折后,点B落在x轴上,记作B1点,求B1点的坐标;
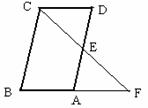 若使∠F=∠BCF,□ABCD的边长之间还需要加一个什么条件?请你补上这个条件,并证明.(不要再添辅助线)
若使∠F=∠BCF,□ABCD的边长之间还需要加一个什么条件?请你补上这个条件,并证明.(不要再添辅助线)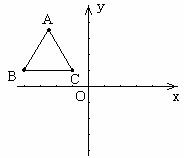 (4)探索:能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定回答,并指出这时的旋转中心和旋转的角度;你若认为不能,请作出否定回答(不必说明理由).
(4)探索:能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定回答,并指出这时的旋转中心和旋转的角度;你若认为不能,请作出否定回答(不必说明理由).