（2005•奉贤区一模）下列能判别两圆的位置关系是外切的是（　　）

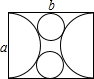（2012•宁波）如图，用邻边分别为a，b（a＜b）的矩形硬纸板裁出以a为直径的两个半圆，再裁出与矩形的较长边、两个半圆均相切的两个小圆．把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽（拼接处材料忽略不计），则a与b满足的关系式是（　　）

圆的切线
[1]定义：和圆有的直线叫圆的切线．
[2]判定：（1）到圆心的距离等于这个圆的的直线是圆的切线；
（2）经过半径并且这条半径的直线是圆的切线．
[3]性质：（1）圆的切线过的半径．
（2）从圆外一点引圆的两条切线，它们的切线长，圆心和这个点的连线平分．（切线长定理）
结论：P是⊙O外一点，PA、PB分别切⊙O于A、B，C是弧AB上一点，DE切⊙O于C交PA、PB于D、E，则△PDE的周长为．

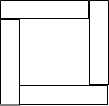小明同学用四张长为x、宽为y的长方形卡片，拼出如图所示的包含两个正方形的图形（任两张相邻的
卡片之间没有重叠，没有空隙）．
①图中小正方形的边长是
②通过计算小正方形面积，可推出（x+y）²，xy，（x-y）²三者的等量关系式为：
③参用②中的结论，试求：当a+b=6，ab=7时（a-b）²的值．

17、已知直角三角形的斜边长c和直角边长a是两个连续整数，则另一个直角边长的平方等于（　　）