0 447189 447197 447203 447207 447213 447215 447219 447225 447227 447233 447239 447243 447245 447249 447255 447257 447263 447267 447269 447273 447275 447279 447281 447283 447284 447285 447287 447288 447289 447291 447293 447297 447299 447303 447305 447309 447315 447317 447323 447327 447329 447333 447339 447345 447347 447348
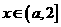 时,
时,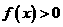 ,
,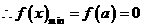 ;
;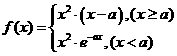 ,求函数f(x)在
,求函数f(x)在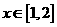 时的最小值。
时的最小值。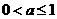 时,
时,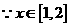 ,
,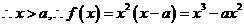 ,
,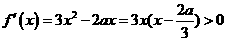 ,
, 时是增函数,
时是增函数, ;
;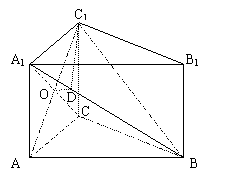 解法(一):(1)在△ABC中
解法(一):(1)在△ABC中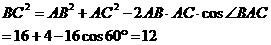
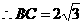
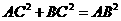
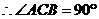 ,即
,即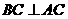 ,
,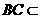 平面ABC,
平面ABC,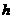 ,则
,则
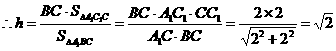 ………………………8分
………………………8分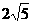 ,BC=
,BC=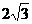 ,A1C=
,A1C=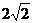 ,A1O=
,A1O=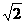 。
。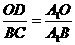 得:
得: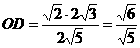
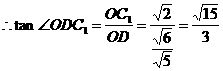
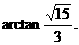 ……………………………………12分
……………………………………12分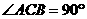 ,然后以C为原点,分别以CA、CB、CC1为
,然后以C为原点,分别以CA、CB、CC1为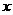 轴、
轴、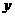 轴、
轴、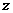 轴建立空间直角坐标系(略)
轴建立空间直角坐标系(略) (本小题满分12分)
(本小题满分12分)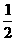 ,构造数列
,构造数列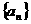 ,使得
,使得 ,记
,记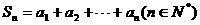 。
。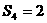 的概率;
的概率;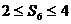 的概率。
的概率。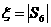 ,求
,求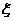 的数学期望。
的数学期望。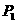
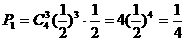
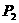 。
。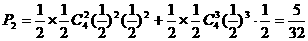
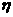 次,则
次,则 -B(4,
-B(4,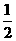 ),
),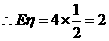 ,
,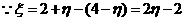 ,
,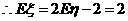 。
。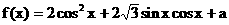 (
(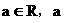 为常数)
为常数)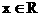 ,求
,求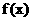 的最小正周期;
的最小正周期;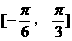 上最大值与最小值之和为3,求a的值。
上最大值与最小值之和为3,求a的值。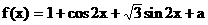 ……3分
……3分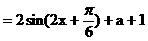 ……5分
……5分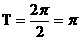 ……6分
……6分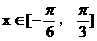 知
知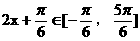 ……8分
……8分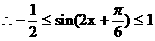
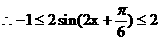 ……10分
……10分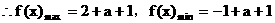
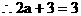 ,解得
,解得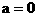 ……12分
……12分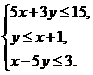 ,若使z=x+ky最小的最优解有无穷多个,则k的值是__-1____。
,若使z=x+ky最小的最优解有无穷多个,则k的值是__-1____。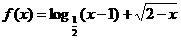 的定义域为_
的定义域为_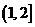 ;值域为
;值域为 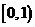 。
。