摘要:已知 (Ⅰ)求的值, (Ⅱ)求的值. 解:(Ⅰ)由.得.所以=. (Ⅱ)∵.∴. 在添加剂的搭配使用中.为了找到最佳的搭配方案.需要对各种不同的搭配方式作比较.在试制某种牙膏新品种时.需要选用两种不同的添加剂.现有芳香度分别为0.1.2.3.4.5的六种添加剂可供选用.根据试验设计原理.通常首先要随机选取两种不同的添加剂进行搭配试验. (Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率, (Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率, 解:设“所选用的两种不同的添加剂的芳香度之和等于4 的事件为A.“所选用的两种不同的添加剂的芳香度之和不小于3 的事件为B (Ⅰ)芳香度之和等于4的取法有2种:..故. (Ⅱ)芳香度之和等于1的取法有1种:,芳香度之和等于2的取法有1种:.故. 如图.P是边长为1的正六边形ABCDEF所在平面外一点..P在平面ABC内的射影为BF的中点O. (Ⅰ)证明⊥, (Ⅱ)求面与面所成二面角的大小. 解:(Ⅰ)在正六边形ABCDEF中.为等腰三角形. ∵P在平面ABC内的射影为O.∴PO⊥平面ABF.∴AO为PA在平面ABF内的射影,∵O为BF中点.∴AO⊥BF.∴PA⊥BF. (Ⅱ)∵PO⊥平面ABF.∴平面PBF⊥平面ABC,而O为BF中点.ABCDEF是正六边形 .∴A.O.D共线.且直线AD⊥BF.则AD⊥平面PBF,又∵正六边形ABCDEF的边长为1.∴... 过O在平面POB内作OH⊥PB于H.连AH.DH.则AH⊥PB.DH⊥PB.所以为所求二面角平面角. 在中.OH=.=. 在中., 而 (Ⅱ)以O为坐标原点.建立空间直角坐标系.P.A(0.,0).B(.0,0).D.∴.. 设平面PAB的法向量为.则..得., 设平面PDB的法向量为.则..得., 设函数.已知是奇函数. (Ⅰ)求.的值. (Ⅱ)求的单调区间与极值. 证明(Ⅰ)∵.∴.从而=是一个奇函数.所以得.由奇函数定义得, 知.从而.由此可知. 和是函数是单调递增区间, 是函数是单调递减区间, 在时.取得极大值.极大值为.在时.取得极小值.极小值为. 在等差数列中..前项和满足条件. (Ⅰ)求数列的通项公式, (Ⅱ)记.求数列的前项和. 解:(Ⅰ)设等差数列的公差为,由得:.所以.即.又=.所以. (Ⅱ)由.得.所以. 当时., 当时. . 即. 如图.F为双曲线C:的右焦点.P为双曲线C右支上一点.且位于轴上方.M为左准线上一点.为坐标原点.已知四边形为平行四边形.. (Ⅰ)写出双曲线C的离心率与的关系式, (Ⅱ)当时.经过焦点F且平行于OP的直线交双曲线于A.B点.若.求此时的双曲线方程. 解:∵四边形是.∴.作双曲线的右准线交PM于H.则.又.. (Ⅱ)当时....双曲线为.设P.则..所以直线OP的斜率为.则直线AB的方程为.代入到双曲线方程得:. 又.由得:.解得.则.所以为所求.
网址:http://m.1010jiajiao.com/timu3_id_4468520[举报]
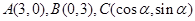
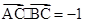 ,求
,求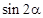 的值;
的值;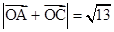 ,其中
,其中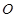 是原点,且
是原点,且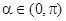 ,求
,求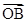 与
与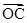 的夹角。
的夹角。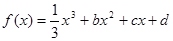 的图象过点(0,3),且在
的图象过点(0,3),且在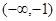 和
和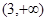 上为增
上为增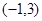 上为减函数.
上为减函数.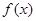 的解析式;
的解析式;
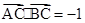 ,求
,求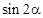 的值;
的值;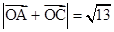 ,其中
,其中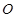 是原点,且
是原点,且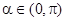 ,求
,求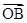 与
与 的夹角。
的夹角。