19. 如图,正方形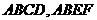 的边长都是1,而且平面
的边长都是1,而且平面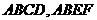 互相垂直。点
互相垂直。点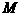 在
在 上移动,点
上移动,点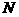 在
在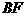 上移动,若
上移动,若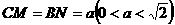 。
。
(1)求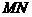 的长;
的长;
(2)当 为何值时,
为何值时,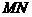 的长最小;
的长最小;
|









 (3)当
(3)当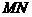 长最小时,求面
长最小时,求面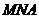 与面
与面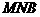 所成的二面角
所成的二面角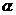 的大小。
的大小。
19. 如图,正方形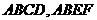 的边长都是1,而且平面
的边长都是1,而且平面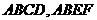 互相垂直。点
互相垂直。点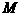 在
在 上移动,点
上移动,点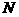 在
在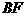 上移动,若
上移动,若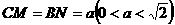 。
。
(1)求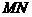 的长;
的长;
(2)当 为何值时,
为何值时,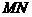 的长最小;
的长最小;
|










 (3)当
(3)当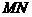 长最小时,求面
长最小时,求面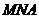 与面
与面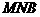 所成的二面角
所成的二面角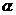 的大小。
的大小。