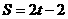2、今有一组实验数据如下:
 |
1.993 |
3.002 |
4.001 |
5.032 |
6.121 |
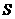 |
1.501 |
4.413 |
7.498 |
12.04 |
17.98 |
现准备用下列函数中的一个,近似地表示数据满足的规律,其中接近的是( )
A、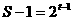 B、
B、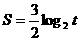 C、
C、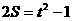 D、
D、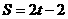
2、今有一组实验数据如下:
 |
1.993 |
3.002 |
4.001 |
5.032 |
6.121 |
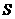 |
1.501 |
4.413 |
7.498 |
12.04 |
17.98 |
现准备用下列函数中的一个,近似地表示数据满足的规律,其中接近的是( )
A、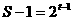 B、
B、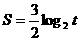 C、
C、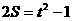 D、
D、