0 445972 445980 445986 445990 445996 445998 446002 446008 446010 446016 446022 446026 446028 446032 446038 446040 446046 446050 446052 446056 446058 446062 446064 446066 446067 446068 446070 446071 446072 446074 446076 446080 446082 446086 446088 446092 446098 446100 446106 446110 446112 446116 446122 446128 446130 446136 446140 446142 446148 446152 446158 446166 447348
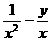 的取值范围是
( )。
的取值范围是
( )。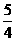 ](D)(-∞, -2]∪[2, +∞)
](D)(-∞, -2]∪[2, +∞)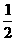 ,
, 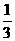 ), 则a-b等于
( )。
), 则a-b等于
( )。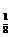 x)>0的x的取值范围是
(
)。
x)>0的x的取值范围是
(
)。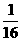 , 1) (B)(1, +∞) (C)(
, 1) (B)(1, +∞) (C)(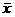 ,若a是不等于
,若a是不等于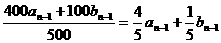 ; bn=
; bn=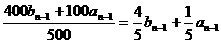
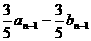 =
=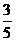 (
(
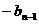 )(n≥2),∴{an-bn}是等比数列。又a1-b1=-10%,
)(n≥2),∴{an-bn}是等比数列。又a1-b1=-10%,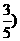 n-1.……(1)
n-1.……(1)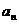
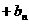 =
=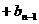 =…= a1+b1=30%,……(2)
=…= a1+b1=30%,……(2)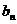 =(
=(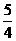 an-1-200,设an +λ=
an-1-200,设an +λ=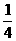 λ,
λ,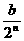 件,(n∈N*)。
件,(n∈N*)。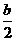 +
+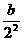 +
+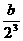 +…+
+…+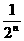 )
) ,相加得Sn-S0=
,相加得Sn-S0=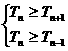 ,得
,得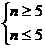 ,故n=5,此时s=7875。
,故n=5,此时s=7875。