摘要:已知...求tg的值. 四棱锥P-ABCD中.底面ABCD是菱形.并且∠DAB=60°.侧面PAD为正三角形.其所在平面垂直于底面ABCD. (I)求证:AD⊥PB, (Ⅱ)求二面角A-BC-P的大小, (Ⅲ)设E为BC边的中点.F为PC中点.求证:平面DEF⊥平面ABCD. 某家用电器的生产厂家根据其产品在市场上的销售情况.决定对原来以每件2000元出售的一种产品进行调价.并按新单价的八折优惠销售.结果每件产品仍可获得实际销售价20%的利润.已知该产品每件的成本是原销售单价的60%. (I)求调整后这种产品的新单价是每件多少元?让利后的实际销售价是每件多少元? (Ⅱ)为使今年按新单价让利销售后的利润总额不低于20万元.今年至少应销售这种产品多少件? (每件产品利润=每件产品的实际售价-每件产品的成本价) 函数y=kx的图象与函数的图象交于.两点(在线段上.O为坐标原点).过.作x轴的垂线.垂足分别为M.N.并且.分别交函数的图象于.两点. (I)求证:是的中点, (Ⅱ)若平行于x轴.求四边形的面积. 已知数列是由正数组成的等差数列.是其前n项的和.并且.. (I)求数列的通项公式, (Ⅱ)证明:不等式对一切n∈N均成立, (Ⅲ)若数列的通项公式满足.是其前n项的和.试问整数是否是数列中的项?若是.则求出相应的项数,若不是.请说明理由. 已知椭圆C的方程为.双曲线的两条渐近线为..过椭圆C的右焦点F作直线l.使.又l与交于P点.设l与椭圆C的两个交点由上至下依次为A.B. (I)当与夹角为60°.双曲线的焦距为4时.求椭圆C的方程及离心率, (Ⅱ)求的最大值.
网址:http://m.1010jiajiao.com/timu3_id_4460861[举报]
(本小题满分14分)甲、乙两间商店购进同一种商品的价格均为每件30元,销售价均为每件50元.根据前5年的有关资料统计,甲商店这种商品的年需求量![]() 服从以下分布:
服从以下分布:
|
| 10 | 20 | 30 | 40 | 50 |
|
| 0.15 | 0.20 | 0.25 | 0.30 | 0.10 |
乙商店这种商品的年需求量![]() 服从二项分布
服从二项分布![]() .
.
若这种商品在一年内没有售完,则甲商店在一年后以每件25元的价格处理;乙商店一年后剩下的这种商品第1件按25元的价格处理,第2件按24元的价格处理,第3件按23元的价格处理,依此类推.今年甲、乙两间商店同时购进这种商品40件,根据前5年的销售情况,请你预测哪间商店的期望利润较大?
查看习题详情和答案>>(本小题满分15分)
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.

(1)将y表示成x的函数;
(11)讨论(1)中函数的单调性,并判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
查看习题详情和答案>>
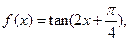 ,
,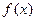 的定义域与最小正周期;
的定义域与最小正周期; ,若
,若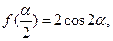 求
求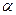 的大小.
的大小.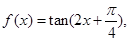 ,
,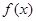 的定义域与最小正周期;
的定义域与最小正周期;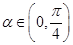 ,若
,若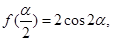 求
求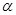 的大小.
的大小.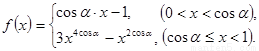 (其中
(其中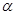 为锐角三角形的内角)且满足
为锐角三角形的内角)且满足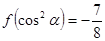 .
.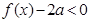 恒成立,求
恒成立,求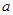 的取值范围.
的取值范围.