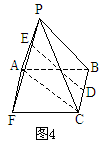0 446032 446040 446046 446050 446056 446058 446062 446068 446070 446076 446082 446086 446088 446092 446098 446100 446106 446110 446112 446116 446118 446122 446124 446126 446127 446128 446130 446131 446132 446134 446136 446140 446142 446146 446148 446152 446158 446160 446166 446170 446172 446176 446182 446188 446190 446196 446200 446202 446208 446212 446218 446226 447348
 的准线方程为
的准线方程为 B.y=
B.y=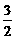
 在
在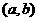 单调递增,在
单调递增,在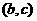 单调递增,又知函数在
单调递增,又知函数在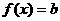 处连续,因此
处连续,因此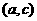 单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为一个区间。
单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为一个区间。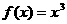 (
(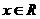 )的单调区间。
)的单调区间。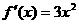 ,当
,当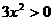 ,即
,即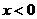 或
或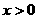 时,
时,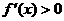 ∴
∴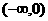 ,
,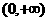 上为增函数,又∵
上为增函数,又∵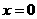 处连续,且相邻区间的单调性又相同,∴
处连续,且相邻区间的单调性又相同,∴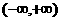 上为增函数。
上为增函数。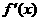 ,令
,令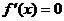 ,解方程求分界点;
,解方程求分界点;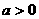 ,
,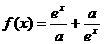 是
是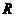 上的偶函数。
上的偶函数。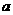 的值;(II)证明
的值;(II)证明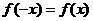 ,即
,即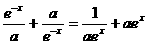 ,
,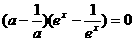 对一切
对一切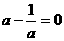 ,
,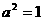 ,又∵
,又∵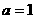 。
。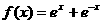 ,得
,得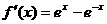
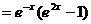 ,
,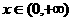 时,有
时,有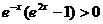 ,此时
,此时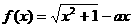 ,其中
,其中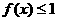 ;(II)证明:当
;(II)证明:当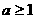 时,函数
时,函数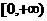 上是单调函数。
上是单调函数。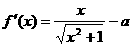 (i)当
(i)当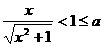 ,此时
,此时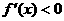 ,函数
,函数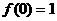 ,因此,当且仅当
,因此,当且仅当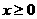 时,
时,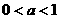 时,解不等式
时,解不等式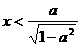 ,
,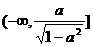 上是单调递减函数。解方程
上是单调递减函数。解方程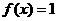 ,得
,得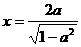 ,
,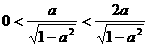 , ∴当且仅当
, ∴当且仅当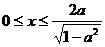 时,
时,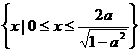 ;
;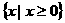 。
。
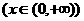 的单调区间。(2003年高考(理)19题)
的单调区间。(2003年高考(理)19题)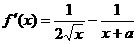 (
(
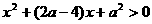 ,
,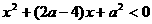 ,
,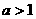 时,对所有
时,对所有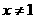 ,恒有
,恒有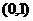 单调递增,在
单调递增,在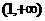 单调递增,
单调递增,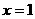 处连续,因此
处连续,因此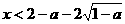 或
或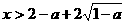 ,因此,函数
,因此,函数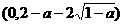 单调递增,在
单调递增,在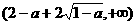 单调递增,令
单调递增,令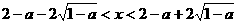 ,
,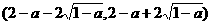 上单调递减。
上单调递减。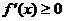 与
与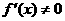 时,
时,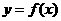 在某个区间内可导。
在某个区间内可导。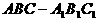 的侧面
的侧面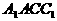 与底面垂直,
与底面垂直,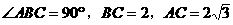 且
且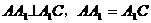 ,(如图7)
,(如图7)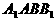 的距离。
的距离。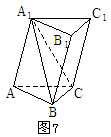
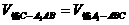 得:
得: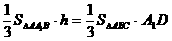
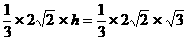
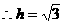 为所求
为所求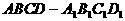 是棱长为a的正方体,E、F分别为棱
是棱长为a的正方体,E、F分别为棱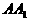 与
与 的中点,求四棱锥
的中点,求四棱锥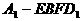 的体积。
的体积。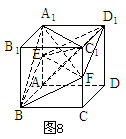
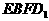 为菱形,连结
为菱形,连结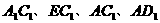 ,则
,则
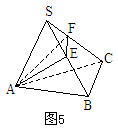
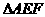 周长最小值问题就转化成了求A、A'两点间的最短距离。
周长最小值问题就转化成了求A、A'两点间的最短距离。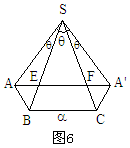
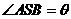 ,则由余弦定理得
,则由余弦定理得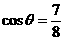
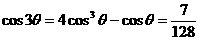
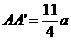
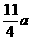
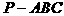 中,已知
中,已知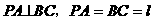 ,PA、BC的公垂线段
,PA、BC的公垂线段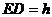 ,求证三棱锥
,求证三棱锥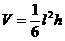 。
。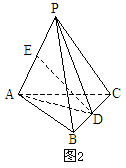
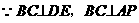
 平面APD,又
平面APD,又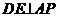 ,
,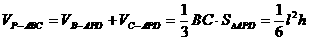
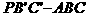 ,连结EC、EB,则易证AP⊥平面EBC,
,连结EC、EB,则易证AP⊥平面EBC,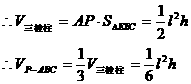
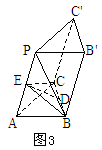
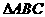 补成平行四边形ABCF,可利用
补成平行四边形ABCF,可利用