0 138897 138905 138911 138915 138921 138923 138927 138933 138935 138941 138947 138951 138953 138957 138963 138965 138971 138975 138977 138981 138983 138987 138989 138991 138992 138993 138995 138996 138997 138999 139001 139005 139007 139011 139013 139017 139023 139025 139031 139035 139037 139041 139047 139053 139055 139061 139065 139067 139073 139077 139083 139091 447348

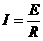 (1分)
(1分)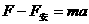 (2分)
(2分)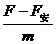 = 3m/s2
(1分)
= 3m/s2
(1分)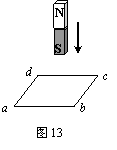 如图13所示,水平桌面上有一质量为m的铜质矩形线圈abcd,当一竖直放置的条形磁铁的S极从线圈正上方快速靠近线圈时,流过ab边的电流方向为
;若线圈始终不动,线圈受到的支持力FN与自身重力间的关系是FN
mg(选填“>”、“<”或“=”)。
如图13所示,水平桌面上有一质量为m的铜质矩形线圈abcd,当一竖直放置的条形磁铁的S极从线圈正上方快速靠近线圈时,流过ab边的电流方向为
;若线圈始终不动,线圈受到的支持力FN与自身重力间的关系是FN
mg(选填“>”、“<”或“=”)。
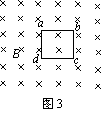 如图3所示,在垂直于纸面的范围足够大的匀强磁场中,有一个矩形闭合线框abcd,线框平面与磁场垂直。在下列哪种情况,可使线框中产生感应电流
如图3所示,在垂直于纸面的范围足够大的匀强磁场中,有一个矩形闭合线框abcd,线框平面与磁场垂直。在下列哪种情况,可使线框中产生感应电流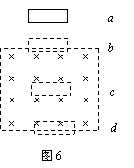 D.线框绕过d点与纸面垂直的轴,沿纸面顺时针转动
D.线框绕过d点与纸面垂直的轴,沿纸面顺时针转动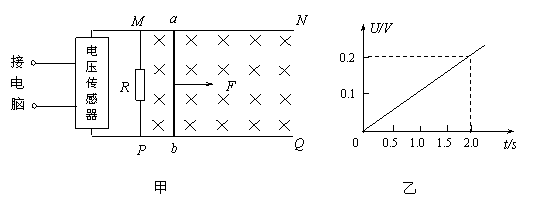 (3)如果水平外力从静止开始拉动杆2s所做的功为0.3J,求回路中定值电阻R上产生的焦耳热是多少。
(3)如果水平外力从静止开始拉动杆2s所做的功为0.3J,求回路中定值电阻R上产生的焦耳热是多少。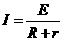 ……………………1分
……………………1分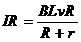 ……………………1分
……………………1分 ,……………………
1分
,……………………
1分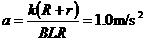 。……1分
。……1分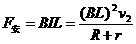 ……………………1分
……………………1分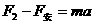 ,……………………1分
,……………………1分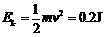 ……………………1分
……………………1分
 ……………………1分
……………………1分 ……………………1分
……………………1分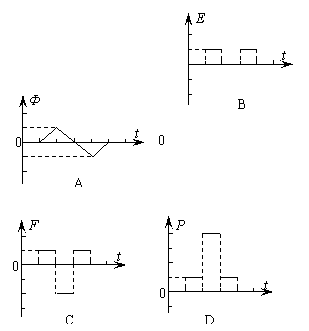
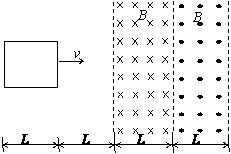
 如图所示,在粗糙绝缘水平面上有一正方形闭合金属线框abcd,其边长为l、质量为m,金属线框与水平面的动摩擦因数为μ。虚线框a′b′c′d′内有一匀强磁场,磁场方向竖直向下。开始时金属线框的ab边与磁场的d′c′边重合。现使金属线框以初速度v0沿水平面滑入磁场区域,运动一段时间后停止,此时金属线框的dc边与磁场区域的d′c′边距离为l。在这个过程中,金属线框产生的焦耳热为
如图所示,在粗糙绝缘水平面上有一正方形闭合金属线框abcd,其边长为l、质量为m,金属线框与水平面的动摩擦因数为μ。虚线框a′b′c′d′内有一匀强磁场,磁场方向竖直向下。开始时金属线框的ab边与磁场的d′c′边重合。现使金属线框以初速度v0沿水平面滑入磁场区域,运动一段时间后停止,此时金属线框的dc边与磁场区域的d′c′边距离为l。在这个过程中,金属线框产生的焦耳热为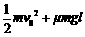 B.
B.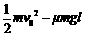 C.
C.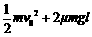 D.
D.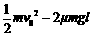
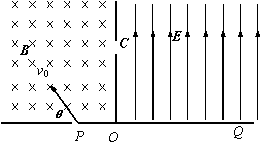 如图所示的区域中,左边为垂直纸面向里的匀强磁场,磁感应强度为 B ,右边是一个电场强度大小未知的匀强电场,其方向平行于OC且垂直于磁场方向.一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度V0沿垂直于磁场方向进人匀强磁场中,初速度方向与边界线的夹角θ=600 ,粒子恰好从C孔垂直于OC射入匀强电场,最后打在Q点,已知OQ= 2 OC ,
如图所示的区域中,左边为垂直纸面向里的匀强磁场,磁感应强度为 B ,右边是一个电场强度大小未知的匀强电场,其方向平行于OC且垂直于磁场方向.一个质量为m 、电荷量为-q 的带电粒子从P孔以初速度V0沿垂直于磁场方向进人匀强磁场中,初速度方向与边界线的夹角θ=600 ,粒子恰好从C孔垂直于OC射入匀强电场,最后打在Q点,已知OQ= 2 OC ,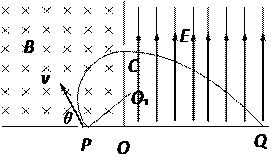 (1)画出粒子运动的轨迹如图示的三分之一圆弧
(1)画出粒子运动的轨迹如图示的三分之一圆弧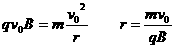 ……………………2分
……………………2分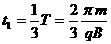 ……………………1分
……………………1分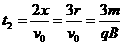 …………………………………………1分
…………………………………………1分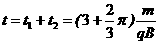 …………………………1分
…………………………1分 场中类平抛运动
场中类平抛运动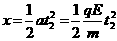 ……1分
……1分 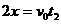 ……1分
……1分 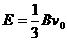 …………………1分
…………………1分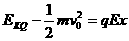 …………2分
解得粒子到达Q点时的动能为
…………2分
解得粒子到达Q点时的动能为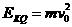 ……1
……1