0 138791 138799 138805 138809 138815 138817 138821 138827 138829 138835 138841 138845 138847 138851 138857 138859 138865 138869 138871 138875 138877 138881 138883 138885 138886 138887 138889 138890 138891 138893 138895 138899 138901 138905 138907 138911 138917 138919 138925 138929 138931 138935 138941 138947 138949 138955 138959 138961 138967 138971 138977 138985 447348
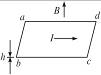
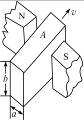
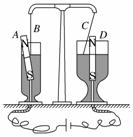 物理学家法拉第在研究电磁学时,亲手做过许多实验,如图2所示的实验就是著名的电磁旋转实验,这种现象是:如果载流导线附近只有磁铁的一个极,磁铁就会围绕导线旋转;反之,载流导线也会围绕单独的某一磁极旋转.这一装置实际上就是最早的电动机.图中A是可动磁铁,B是固定导线,C是可动导线,D是固定磁铁.图中黑色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上.请你判断这时自上向下看,A和C转动方向为
( )
物理学家法拉第在研究电磁学时,亲手做过许多实验,如图2所示的实验就是著名的电磁旋转实验,这种现象是:如果载流导线附近只有磁铁的一个极,磁铁就会围绕导线旋转;反之,载流导线也会围绕单独的某一磁极旋转.这一装置实际上就是最早的电动机.图中A是可动磁铁,B是固定导线,C是可动导线,D是固定磁铁.图中黑色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上.请你判断这时自上向下看,A和C转动方向为
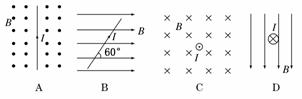
( )
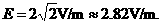
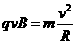
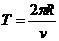
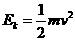
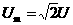
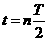
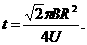

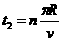
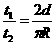 ,又R>>d,所以
,又R>>d,所以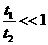 ,因此t1可忽略不计.
,因此t1可忽略不计.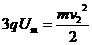
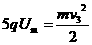
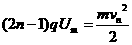
 (n取1,2,3,…).
(n取1,2,3,…).
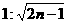
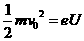
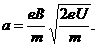
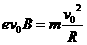 得
得
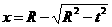
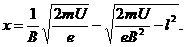
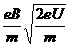
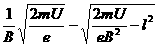
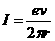 ①
①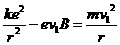 ②
②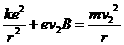 ③
③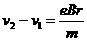 ④
④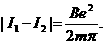
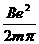
 ,
,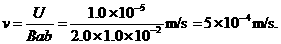
 即驱动力对液体造成的压强差为
即驱动力对液体造成的压强差为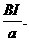
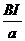
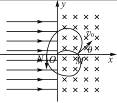
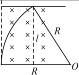
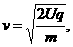 带电粒子以该速度进入对撞机的环状空腔内,且在圆环内做半径确定的圆周运动,因此
带电粒子以该速度进入对撞机的环状空腔内,且在圆环内做半径确定的圆周运动,因此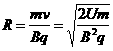 ,对于给定的加速电压,即U一定,则带电粒子的比荷q/m越大,磁感应强度B应越小,A错误,B正确;带电粒子运动周期为
,对于给定的加速电压,即U一定,则带电粒子的比荷q/m越大,磁感应强度B应越小,A错误,B正确;带电粒子运动周期为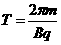 ,与带电粒子的速度无关,当然就与加速电压U无关,因此,对于给定的带电粒子和磁感应强度B,不管加速电压U多大,粒子运动的周期都不变.
,与带电粒子的速度无关,当然就与加速电压U无关,因此,对于给定的带电粒子和磁感应强度B,不管加速电压U多大,粒子运动的周期都不变.
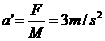 ,B、D正确.
,B、D正确.