12.(8分)(2010年上海师大附中)在右图所示的实验装置中,横杆能够绕竖直轴旋转,横杆在转动过程中,由于摩擦阻力的作用,横杆会越转越慢.在横杆的一端装有宽度为d=0.005 m的竖直“挡光圆柱”,当“挡光圆柱”通过光电门时,光电门就记录挡光的时间间隔,“挡光圆柱”宽度与挡光时间之比,可以近似认为是“挡光圆柱”在该时刻的速度.横杆每转一圈,光电门就记录一次“挡光圆柱”挡光时间.在一次实验中记录下横杆转动圈数n和每次挡光的时间t,并计算出“挡光圆柱”在该时刻的速度以及速度的平方(部分数据如表中所示).请计算表中当n=5时,v2=________m2/s2;如果继续测量“挡光圆柱”的速度,那么当n=15时,“挡光圆柱”的速度为__________m/s;“挡光圆柱”速度大小v与横杆转动圈数n的关系为____________
|
n |
t(10-3s) |
v=d/t(m/s) |
v2(m2/s2) |
|
1 |
2.778 |
1.80 |
3.24 |
|
2 |
2.826 |
… |
3.13 |
|
3 |
2.877 |
… |
3.02 |
|
4 |
2.931 |
… |
2.91 |
|
5 |
2.988 |
… |
|
|
6 |
3.049 |
… |
2.69 |
|
7 |
3.113 |
… |
2.58 |
|
8 |
3.181 |
… |
2.47 |
|
9 |
3.255 |
… |
2.36 |
|
10 |
3.333 |
… |
2.25 |
|
… |
… |
… |
… |
[答案] 2.80 m2/s2 1.30 m/s
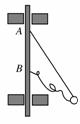 (10分)如右图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为L,B处绳长为L,两根绳能承受的最大拉力均为2mg,转轴带动小球转动.则:
(10分)如右图所示,一个质量为m的小球由两根细绳拴在竖直转轴上的A、B两处,AB间距为L,A处绳长为L,B处绳长为L,两根绳能承受的最大拉力均为2mg,转轴带动小球转动.则:
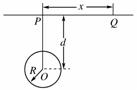
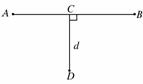 (10分)(2010年江苏无锡调研)早期人类狩猎的主要工具为标枪.如图,一只野兔(高度不计)以速度v1=20 m/s沿AB向右匀速奔跑,猎手隐藏在与直线AB相距d=9.0 m处的D点准备投掷.当野兔到达C点时,猎手沿水平方向投出一支标枪,标枪的投出点距离地面高度为h=1.8 m,忽略空气阻力,重力加速度g=10 m/s2.若刚好射中野兔,求:
(10分)(2010年江苏无锡调研)早期人类狩猎的主要工具为标枪.如图,一只野兔(高度不计)以速度v1=20 m/s沿AB向右匀速奔跑,猎手隐藏在与直线AB相距d=9.0 m处的D点准备投掷.当野兔到达C点时,猎手沿水平方向投出一支标枪,标枪的投出点距离地面高度为h=1.8 m,忽略空气阻力,重力加速度g=10 m/s2.若刚好射中野兔,求: